Число x называется неподвижной точкой (fixed point) функции f, если оно удовлетворяет уравнению f(x) = x. Для некоторых функций f можно найти неподвижную точку, начав с какого-то значения и применяя f многократно:
f(x), f(f(x)), f(f(f(x))), . . .
— пока значение не перестанет сильно изменяться.
*-Нравится статья? Кликни по рекламе! :)
С помощью этой идеи мы можем составить процедуру fixed-point, которая в качестве аргументов принимает функцию и начальное значение и производит приближение к неподвижной точке функции. Мы многократно применяем функцию, пока не найдем два последовательных значения, разница между которыми меньше некоторой заданной чувствительности:
def fixedPoint(f, firstGuess):
def closeEnaught(x,y):
if abs(x-y)<0.001:
return 1
return 0
def tryF(guess):
next=f(guess)
if closeEnaught(guess, next):
return next
return tryF(next)
return tryF(firstGuess)
Подобным образом можно найти решение уравнения y = sin(y) + cos(y): fixedPoint(lambda y: math.sin(y)+math.cos(y), 1.0)
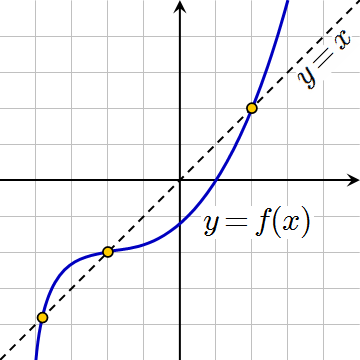
Важно: нужно понимать, что для данного метода очень важно первое приближение, которое мы выберем. Это связано с направлением роста преобразований:
f(x), f(f(x)), f(f(f(x))), . . .
Этот процесс можно представить, как скольжение по графику. Для примера можно рассмотреть y=f(x)=x2. Сразу на ум приходит 2 стационарные точки - 0 и 1. Если возьмем первое приближение>1, то каждая такая подстановка будет больше предыдущей, что характеризует растущий график и мы не найдем стационарной точки. Если возьмем 0<приближение<1, то каждое новое значение будет меньше предыдущего и так мы найдем стационарную точку=0. Таким образом найти 1 можно лишь попав в неё сразу, т.е. выбрав приближение=1.0;
y → x/y, и, следовательно, мы можем попытаться вычислять квадратные корни так:
def sqrt(x):
return fixedPoint(lambda y: x/y, 1.0)
К сожалению, этот поиск неподвижной точки не сходится. Рассмотрим исходное значение y1. Следующее значение равно y2 = x/y1, а следующее за ним y3 = x/y1 =x/(x/y1) = y1. В результате выходит бесконечный цикл, в котором два значения y1 и y2 повторяются снова и снова, прыгая вокруг правильного ответа.Один из способов управлять такими прыжками состоит в том, чтобы заставить значения изменяться не так сильно. Поскольку ответ всегда находится между текущим значением y и x/y, мы можем взять новое значение, не настолько далекое от y, как x/y, взяв среднее между ними, так что следующее значение будет не x/y, а 1/2(y +x/y). Процесс получения такой последовательности есть всего лишь процесс поиска неподвижной
точки y →1/2(y + x/y).
def average(x, y):
return (x+y)/2
def sqrt(x):
return fixedPoint(lambda y: average(y,x/y), 1.0)
Интересно: Заметим, что y =1/2(y + x/y) всего лишь простая трансформация уравнения y = x/y; чтобы ее получить, добавьте y к обоим частям уравнения и поделите пополам.Этот подход с усреднением последовательных приближений к решению, метод, который называют торможение усреднением (average damping), часто помогает достичь сходимости при поисках неподвижной точки.
Используемая литература:
Комментариев нет:
Отправить комментарий