Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел.
*-Нравится статья? Кликни по рекламе! :)
Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Впервые, с нормальным вариантом реализации я встретился на 28 стр. 1 тома "Искусства программирования" Д.Э.Кнута.
Позже я пересекся с ним в видео лекции http://www.intuit.ru/department/algorithms/introprogalgo/4/
Там он проходил в разделе рекурсии, и было объяснено, что с каждой итерациеё число сокращается более чем в 2-е из-за чего max за logM+logN итераций НОД будет найден.
Есть значит такой вот сайтик http://younglinux.info. Меня отсюда будет интересовать http://younglinux.info/algorithm/euclidean Здесь, кроме всем известного метода, приведен еще и наиболее не практичная версия алгоритма, назовем его, метод последовательной разницы.
Вот что написано в вике на этот счет:
Интересное: Тот факт, что число шагов, затрачиваемых алгоритмом Евклида, растет логарифмически, связан с числами Фибоначчи:
С помощью этой теоремы можно оценить порядок роста алгоритма Евклида. Пусть a будет меньшим из двух аргументов процедуры. Если процесс завершается за k шагов, тогда должно выполняться a>=Fib(k), т.е. приблизительно равно f^5/sqrt(5) - золотое сечение. Следовательно, число шагов k растет как логарифм a(по основанию f)!
Теперь по-поводу тестирования. Для этого я использую стандартный python profile.
Само собой 1 запуск любого из 3-х вариантов будет производителен, посему я сделал это по 2000 раз, чтобы увидеть разницу.
Результат, полностью подтвердил теорию:
Используемая литература:
1.) http://ru.wikipedia.org/wiki/Алгоритм_Евклида
2.) http://ru.wikibooks.org/wiki/Примеры_реализации_алгоритма_Евклида
Позже я пересекся с ним в видео лекции http://www.intuit.ru/department/algorithms/introprogalgo/4/
Там он проходил в разделе рекурсии, и было объяснено, что с каждой итерациеё число сокращается более чем в 2-е из-за чего max за logM+logN итераций НОД будет найден.
Алгоритм Евклида (описание с Вики)
Пусть a и b — целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое rk — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
Тогда НОД(a,b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности.
- a = bq0 + r1
- b = r1q1 + r2
- r1 = r2q2 + r3
- rk − 2 = rk − 1qk − 1 + rk
- rn − 1 = rnqn
Есть значит такой вот сайтик http://younglinux.info. Меня отсюда будет интересовать http://younglinux.info/algorithm/euclidean Здесь, кроме всем известного метода, приведен еще и наиболее не практичная версия алгоритма, назовем его, метод последовательной разницы.
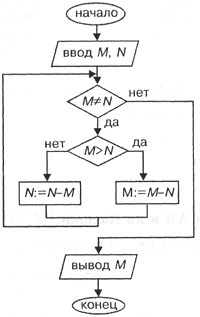
Конкретная реализация алгоритма:Описание алгоритма нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
def gcd(a,b):
while a != b:
if a > b:
a = a - b
else:
b = b - a
print (a)
А вот нормальная его реализация (аналог из видеолекции с применением рекурсии). Тут применена идея поочередного деления, поэтому назовем его , как не трудно догадаться, :)) метод поочередного деления.def gcd(a, b): if b == 0: return a else: return gcd(b, a % b)Так же существует его реализация в не рекурсивном виде
def gcd(a, b):
while b:
a, b = b, a % b
return a
И должен признаться, что с точки зрения производительности он предпочтительнее. Основные причины - стек рекурсиии (т.е. доп. память на хранение и доп. время на доступ к заранее сохраненным данным), об этом вы так же можете услышать из видео лекции. Там же затронули связь НОД и НОК (наименьшее общее кратное).Вот что написано в вике на этот счет:
Наименьшее общее кратное (НОК) двух целых чисел m и n — это наименьшее натуральное число, которое делится на m и n. Обозначается НОК(m,n) или [m,n], а в английской литературе lcm(m,n).Таким образом поиск НОК выглядит следующим образом
НОК для ненулевых чисел m, n всегда существует и связан с НОД следующим соотношением:
def mcd(n,m):
return (n/gcd(n,m))*m
Хочу обратить ваше внимание на то, что сначалы мы делим на НОД а потом умножаем, таким образом мы защищаем себя от переполнения при произведении 2-х больших цифр.Интересное: Тот факт, что число шагов, затрачиваемых алгоритмом Евклида, растет логарифмически, связан с числами Фибоначчи:
Теорема (Ламэ, 1845 г.). Пусть n О N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = F n +2 , b = F n +1 , где F k - k- ое число Фибоначчи.Доказательство можно посмотреть, например, здесь: http://virlib.eunnet.net/books/numbers/text/10.html
С помощью этой теоремы можно оценить порядок роста алгоритма Евклида. Пусть a будет меньшим из двух аргументов процедуры. Если процесс завершается за k шагов, тогда должно выполняться a>=Fib(k), т.е. приблизительно равно f^5/sqrt(5) - золотое сечение. Следовательно, число шагов k растет как логарифм a(по основанию f)!
Теперь по-поводу тестирования. Для этого я использую стандартный python profile.
Само собой 1 запуск любого из 3-х вариантов будет производителен, посему я сделал это по 2000 раз, чтобы увидеть разницу.
Результат, полностью подтвердил теорию:
- Самым медленным оказался метод последовательной разницы 2004 function calls in 3.086 seconds
- Сильно быстрее - метод поочередного деления в рекурсивном виде 13743 function calls (2004 primitive calls) in 0.088 seconds
- Ну и победитель забега - метод поочередного деления в не рекурсивном 2004 function calls in 0.014 seconds
Используемая литература:
1.) http://ru.wikipedia.org/wiki/Алгоритм_Евклида
2.) http://ru.wikibooks.org/wiki/Примеры_реализации_алгоритма_Евклида



![(m,n)\cdot[m,n]=m\cdot n](http://upload.wikimedia.org/math/3/7/e/37e2429cfba5c9489e685df64f7131ef.png)
Комментариев нет:
Отправить комментарий