Вычисление факториала

Мне кажется, что это самый классический алгоритм из существующих. С примером реализации вы наверняка сталкивались и не раз, но для полноты картины, я просто обязан его описать. :))

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

*-Нравится статья? Кликни по рекламе! :)

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок множества из n элементов. Например, для множества {A,B,C,D} существует 4!=24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA 

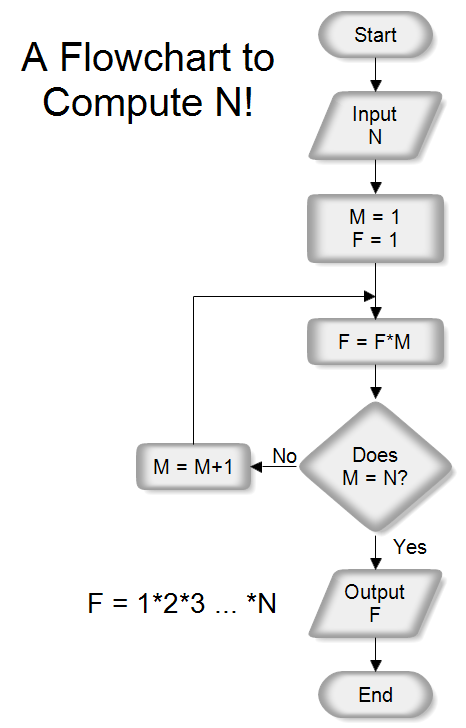
Рекуррентная формула
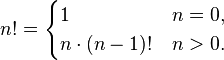 Итак это был тот минимум, который, как я считаю, должен знать любой уважающий себя. и всех тех кто его окружает, человек.
Теперь о реализации алгоритма. Как всегда средств много, от чего мы познакомимся с несколькими из них.
2 классических я возьму с сайта http://younglinux.info/algorithm/factorial
 
С использованием цикла

def fac(n):
    fac = 1 
    i = 0 
    while i < n:
        i += 1
        fac = fac * i
    return fac

С использованием рекурсии

def fac(n):
     if n == 0:
          return 1
     return fac(n-1) * n

И на закуску, высокоинтеллектуальный пример с Вики :))

def factorial(x):
    return 1 if x==0 else reduce(lambda x,y:x*y,xrange(1,x+1))

Ну и теперь самое вкусное и интересное, тестирование!
По их результатам я пришел к выводу, что скорость роста данных алгоритмов приблизительно равна. И по сему результат вычисления 70000! следующий:

• алгоритм с использованием цикла 4 function calls in 11.872 seconds
• алгоритм рекурсивный выбыл, подробнее читать тут
• зверский алгоритм с вики 70004 function calls in 13.211 seconds
• встроенный модуль math.factorial  4 function calls in 8.377 CPU seconds

Вывод таков, что не все нужно брать с википедии :)))
Просто получается многовато вызовов лямбда функций, ведь каждый вызов - это потери, хотим мы этого или нет.
Проблемы, возникшие с рекурсией: по умолчанию, максимальная глубина рекурсии равна 1000. Это ограничение предотвращает переполнение стека при бесконечных рекурсиях.
Я установил при помощи sys.setrecursionlimit(70000) новую глубину, но python падает через пару секунд, все таки нужно помнить, что рекурсия не самая хорошая штука для таких вычислений :((

Почему встроенная функция сильнее, лучше и быстрее? Могу предположить что написание на чистом С ему придает бодрости)))



Вычисление времени выполнения


Для примера разберем рекурсивный вариант. Мы должны с каждой рекурсивной процедурой связать временную функцию T(n), где n определяет объём аргументов процедуры. Затем получить рекуррентное соотношение для T(n). Естественной мерой объёма входных данных для функции fac, является значение n. Обозначим, через T(n) - время выполнения программы.
Время сравнения if имеет порядок роста О(1), а для последней строки О(1)+T(n-1), где О(1)-умножение на n, а T(n-1)-факториала с меньшим входным аргументом. Таким образом для некоторых констант c и d имеем,

Полагая, что n>2 и раскрывая выражение T(n-1)(т.е. подставляя n-1 вместо n и получившееся T(n-1) в предыдущую формулу T(n)), получим T(n)=2с+T(n-2), продолжая такие рассуждения до n-1 раз, получим T(n)=c(n-1)+d. Откуда имеем порядок роста О(n).

UPD:На сайте http://www.iso.ru/journal/articles/199.html
 нашел интересный пример, который, как там и пишут считается скорее шуткой или поводом выиграть спор(на пыво))) у своих друзей:

f = lambda n: n-1 +abs(n-1) and f(n-1)*n or 1

Этот "рецепт" реализует рекурсивное определение функции факториала в виде lambda формы. Поскольку lambda формы должны быть выражениями, это несколько мудрено. Директива if/else не допускается внутри выражения. Все же, закороченная форма идиомы Python для "условного (трехместного) оператора" справляется с этим (другие способы моделирования трехместного оператора, как закороченного, так и нет, см. в "Моделирование трехместного оператора" в "Справочном руководстве по Python").
Реальная проблема, разумеется, состоит в том, что раз сильная сторона lambda в создании безымянных функций, то, как же мы выполняем рекурсию?