Простые числа

Просто́е число́ — это натуральное число, которое имеет ровно два различных натуральных делителя: единицу и самого себя. Все остальные числа, кроме единицы, называются составными.

Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают Решето Эратосфена, решето Сундарама и решето Аткина.

*-Нравится статья? Кликни по рекламе! :)

 Пришла пора, обсудить такую не сложную, на первый взгляд, тему, как простые числа. Рассмотрим алгоритмы нахождения простых чисел до заданного числа n.

Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому.

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
2. Пусть переменная p изначально равна двум — первому простому числу.
3. Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)
4. Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.
5. Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
6. Все не вычеркнутые числа в списке — простые числа.

def primes(n):
    a = [0] * n # создание массива с n количеством элементов
    for i in range(n): # заполнение массива ...
        a[i] = i # значениями от 0 до n-1
     
    # вторым элементом является единица, которую не считают простым числом
    # забиваем ее нулем.
    a[1] = 0
     
    m = 2 # замена на 0 начинается с 3-го элемента (первые два уже нули)
    while m < n: # перебор всех элементов до заданного числа
        if a[m] != 0: # если он не равен нулю, то
            j = m * 2 # увеличить в два раза (текущий элемент простое число)
            while j < n:
                a[j] = 0 # заменить на 0
                j = j + m # перейти в позицию на m больше
        m += 1
     
    # вывод простых чисел на экран (может быть реализован как угодно)
    b = []
    for i in a:
        if a[i] != 0:
            b.append(a[i])
     
    del a
    return b

На практике, алгоритм можно немного улучшить следующим образом. На шаге №3, числа можно вычеркивать, начиная сразу с числа p², потому что все составные числа меньше его уже будут вычеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p² станет больше, чем n. Можно показать, что сложность алгоритма составляет O(nloglogn) операций в модели вычислений RAM, или O(n(logn)(loglogn)) битовых операций.

Еще один вариант исполнения я нашел на сайте http://www.intuit.ru/department/pl/python/2/5.html
Он основан на таком типе данных, как множество, а точнее на операции последовательного вычитания множеств. 

def primes(N):
  """Возвращает все простые от 2 до N"""
  sieve = set(range(2, N))
  for i in range(2, int(math.sqrt(N))):
    if i in sieve:
      sieve -= set(range(2*i, N, i))
  return sieve
print primes(10)

Протестировав 2 этих метода, я получил следующие результаты:
При вычислении простых чисел до 650000, выигрывает алгоритм, оперирующий множествами. Потом, верх берет первый алгоритм. Видимо это связано с внутренней реализацией множеств в python. Если кто-то может описать поподробнее проблему, жду комментариев.


Алгоритм реализации: Решето Сундарама:

В математике решето́ Сундара́ма — детерминированный алгоритм нахождения всех простых чисел до некоторого целого числа . Разработан индийским студентом С. П. Сундарамом в 1934 году.

Обоснование: Алгоритм работает с нечётными натуральными числами большими единицы, представленными в виде 2m+1, где m является натуральным числом. Если число 2m+1 является составным, то оно представляется в виде произведения двух нечётных чисел больших единицы, то есть:

2m+1 = (2i+1)(2j+1)

где i и j — натуральные числа, что также равносильно соотношению:

m = 2ij+i+j.

Таким образом, если из ряда натуральных чисел исключить все числа вида 2ij + i + j, , то для каждого из оставшихся чисел m число 2m+1 обязано быть простым. И, наоборот, если число 2m+1 является простым, то число m невозможно представить в виде 2ij+i+j и, таким образом, m не будет исключено в процессе работы алгоритма.

Описание:
Из ряда натуральных чисел от 1 до N исключаются все числа вида

i + j + 2ij,

где индексы пробегают все натуральные значения, для которых , а именно значения и Затем каждое из оставшихся чисел умножается на 2 и увеличивается на 1. Полученная в результате последовательность представляет собой все нечётные простые числа в отрезке [1,2N+1]. Особенно обратите внимание на то, что входной параметр N, а числа простые находим вплоть до 2N+1!

def good_prime(С):
    D=C/2
    B=C/6
    A=set(range(D))
    for i in xrange(1,B+1):
        for j in xrange(i,(D+i)/(1+2*i)+1):
            A.discard(i+j+2*i*j)
    A=[ 2*x+1 for x in A ]
    return A

Не помню уже, где я  откопал данную реализацию алгоритма, но протестировав его, у меня отвисла челюсть - 87 сек. исполнения тому причина. И в это можно понять: Вы только посмотрите, сколько вычислительных операций происходит в алгоритме! Да и каждый раз удалять элемент из множества, операция не из дешевых.  
Немного прооптимизировав его(путем переписывания алгоритма с вики, приведенного для C++) и результат улучшился до 7.4 сек, что почти на 3сек. лучше предыдущих:

def sundaram(n):
    b=list()
    a = [0] * n

i=k=j=0
    while 3*i+1 < n:
        while k < n and j <= i:
            a[k] = 1
            j+=1
            k = i+j+2*i*j
        i+=1
        k=j=0
    
    for i in xrange(1,n):
          if a[i] == 0:
              b.append(2 * i + 1)
    return b

Если кто-либо поправит код, что он будет сравним с остальными, пишите, буду очень рад.  
Реализация решета Аткина:

В математике решето́ А́ткина — быстрый современный алгоритм нахождения всех простых чисел до заданного целого числа N. Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде a×x²+b×y²). Предыдущие алгоритмы в основном представляли собой различные модификации решета Эратосфена, где использовалось представление чисел в виде редуцированных форм (обычно прозведения x×y). Отдельный этап алгоритма вычеркивает числа, кратные квадратам простых чисел.

Объяснение

• Все числа, равные (по модулю 60) 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, или 58, делятся на два и заведомо не простые. Все числа, равные (по модулю 60) 3, 9, 15, 21, 27, 33, 39, 45, 51, или 57, делятся на три и тоже не являются простыми. Все числа, равные (по модулю 60) 5, 25, 35, или 55, делятся на пять и также не простые. Все эти остатки (по модулю 60) игнорируются.
• Все числа, равные (по модулю 60) 1, 13, 17, 29, 37, 41, 49 или 53, имеют остаток от деления на 4 равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 4x² + y² = n нечётно и само число не кратно никакому квадрату простого числа (en:square-free integer).
• Числа, равные (по модулю 60) 7, 19, 31, или 43, имеют остаток от деления на 6 равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² + y² = n нечётно и само число не кратно никакому квадрату простого.
• Числа, равные (по модулю 60) 11, 23, 47, или 59, имеют остаток от деления на 12 равный 11. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² − y² = n нечётно и само число не кратно никакому квадрату простого.

Ни одно из рассматриваемых чисел не делится на 2, 3, или 5, соответственно, они не могут делиться и на их квадраты. Поэтому проверка, что число не кратно квадрату простого числа, не включает 2², 3², и 5².

Сегментация

Для уменьшения требований к памяти «просеивание» производится порциями (сегментами, блоками), размер которых составляет примерно .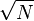

Предпросеивание

Для ускорения работы полная версия алгоритма игнорирует все числа, которые кратны одному из нескольких первых простых чисел (2, 3, 5, 7, …). Это делается путем использования стандартных структур данных и алгоритмов их обработки, предложенных ранее Полом Притчардом (англ. Pritchard, Paul). Они известны под названием англ. wheel sieving. Количество первых простых чисел выбирается в зависимости от заданного числа N. Теоретически предлагается брать первые простые примерно до . Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель . При этом требуется дополнительная память, которая с ростом N ограничена как . Увеличение требований к памяти оценивается как . Версия, представленная на сайте авторов, оптимизирована для поиска всех простых чисел до миллиарда (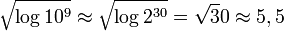), в ней исключаются из вычислений числа кратные двум, трём, пяти и семи (2 × 3 × 5 × 7 = 210).

Оценка сложности

По оценке авторов алгоритм имеет асимптотическую сложность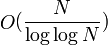 и требует бит памяти. Ранее были известны алгоритмы столь же асимптотически быстрые, но требующие существенно больше памяти: Теоретически в данном алгоритме сочетается максимальная скорость работы при меньших требованиях к памяти. Реализация алгоритма, выполненная одним из авторов, показывает достаточно высокую практическую скорость.

def atkins(limit):
    primes = [False] * limit
    sqrt_limit = int( math.sqrt( limit ) )

    x_limit = int( math.sqrt( ( limit + 1 ) / 2 ) )
    for x in xrange( 1, x_limit ):
        xx = x*x

        for y in xrange( 1, sqrt_limit ):
            yy = y*y

            n = 3*xx + yy
            if n <= limit and n%12 == 7:
                primes[n] = not primes[n]

            n += xx
            if n <= limit and n%12 in (1,5):
                primes[n] = not primes[n]

            if x > y:
                n -= xx + 2*yy
                if n <= limit and n%12 == 11:
                    primes[n] = not primes[n]

    for n in xrange(5,limit):
        if primes[n]:
            for k in range(n*n, limit, n*n):
                primes[k] = False

    return [2,3] + filter(primes.__getitem__, xrange(5, limit))

Жль, но эта реализация проиграла остальным решеткам((( Если кто улучшит этот алгоритм, или напишит ему альтернативу, буду очень рад!

Наблюдения: Из статьи Аткина оказалось, что ассимптотика 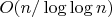подразумевает соответствующее увеличение модуля (12 в обычной реализации). Т.е. если модуль фиксирован, то сложность решета Аткина 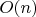. Если теперь учесть потери от блочной реализации, то у Аткина это 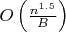, где 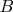- размер блока, а у Эратосфена - 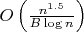. Т.е. у Аткина эти потери начинают превалировать при 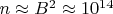в нашем случае, а у Эратосфена - при 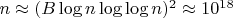. Вывод: как часто бывает, ассимптотически более быстрый и сложный алгоритм на практике проигрывает более простому.   
Использованная литература:

1.  http://younglinux.info/algorithm/sieve 
2.  Простое число 
3.  Решето Эратосфена 
4.  Решето Сундарама 
5.  Решето Аткина