Тест простоты — алгоритм, который по заданному натуральному числу определяет, простое ли это число. Различают детерминированные и вероятностные тесты.*-Нравится статья? Кликни по рекламе! :)
Определение простоты заданного числа в общем случае не такая уж тривиальная задача. Только в 2002 году было доказано, что она полиномиально разрешима. Тем не менее, тестирование простоты значительно легче факторизации заданного числа.
Мы уже разобрали методы выбора всех простых чисел, до определенного, в статье Простые числа. Пришло время рассмотреть ряд алгоритмов, под общим названием - "Тесты простоты":
1.) Перебор делителей:
Перебор делителей — алгоритм факторизации или тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.Описание алгоритма:
Обычно перебор делителей заключается в переборе всех целых (как вариант: простых) чисел от 2 до квадратного корня из факторизуемого числа n и в вычислении остатка от деления n на каждое из этих чисел. Если остаток от деления на некоторое число m равен нулю, то m является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу (если тестируется простота n), либо n сокращается на m и процедура повторяется (если осуществляется факторизация n). По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.
Примечание: если у n есть некоторый делитель p, то n/p так же будет делителем, причем одно из этих чисел не превосходит
 .
. Реализация на Python:
def divider(n):
i = 2
j = 0 # флаг
while i**2 <= n and j != 1:
if n%i == 0:
j = 1
i += 1
if j == 1:
print ("Это составное число")
else:
print ("Это простое число")
2.) Теорема Вильсона
Теорема теории чисел, которая утверждает, что
p — простое число тогда и только тогда, когда (p − 1)! + 1 делится на p |
Реализация:
def prime(n):
if (math.factorial(n-1)+1) % n!=0:
print ("Это составное число")
else:
print ("Это простое число")
3.) Тест простоты Ферма
Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.
Если n — простое число, то an-1  1 mod n.
1 mod n.
Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:
Если n — простое число, то an-11 mod n Если n — составной объект, то возможно, что an-1
1 mod n
больше 1/2. Подводя итог сказанному, выпишем алгоритм теста Ферма.
def primFerma(a,n):
if a**(n-1)%n==1:
print "правдоподобно простое"
else:
print "составное"
Если на выходе этого алгоритма напечатано «составное, а», то мы с определенностью можем заявить, что число n не является простым, и что а свидетельствует об этом факте, т. е. чтобы убедиться в истинности высказывания, нам достаточно провести тест Ферма по основанию а. Такое а называют свидетелем того, что n составное.Если же в результате работы теста мы получим сообщение: «правдоподобно простое», то можно заключить: n — составное с вероятностью ≤
- они нечетны,
- имеют по крайней мере три простых делителя,
- свободны от квадратов1,
- если р делит число Кармайкла N, то р — 1 делит N — 1.
4.)Тест Миллера — Рабина
Вероятностный полиномиальный тест простоты. Тест Миллера — Рабина позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа. Тем не менее тест Миллера — Рабина часто используется в криптографии для получения больших случайных простых чисел.Пусть
Алгоритм был разработан Гари Миллером в 1976 году и модифицирован Майклом Рабином в 1980 году.
 — нечётное число большее 1. Число
— нечётное число большее 1. Число  однозначно представляется в виде
однозначно представляется в виде  , где
, где  нечётно. Целое число
нечётно. Целое число  ,
, 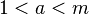 , называется свидетелем простоты числа
, называется свидетелем простоты числа  , если выполняется одно из условий:
, если выполняется одно из условий:- существует целое число
 ,
,  , такое, что
, такое, что 
 различных свидетелей простоты, где
различных свидетелей простоты, где  — функция Эйлера.
— функция Эйлера.Алгоритм Миллера — Рабина параметризуется количеством раундов r. Рекомендуется брать r порядка величины log2(m), где m — проверяемое число.
Для данного m находятся такие целое число s и целое нечётное число t, что m − 1 = 2st. Выбирается случайное число a, 1 < a < m. Если a не является свидетелем простоты числа m, то выдается ответ «m составное», и алгоритм завершается. Иначе, выбирается новое случайное число a и процедура проверки повторяется. После нахождения r свидетелей простоты, выдается ответ «m, вероятно, простое», и алгоритм завершается. Как и для теста Ферма, все числа n > 1, которые не проходят этот тест – составные, а числа, которые проходят, могут быть простыми. И, что важно, для этого теста нет аналогов чисел Кармайкла.
В 1980 году было доказано, что вероятность ошибки теста Рабина-Миллера не превышает 1/4. Таким образом, применяя тест Рабина-Миллера t раз для разных оснований, мы получаем вероятность ошибки 2-2t.
def toBinary(n):
r = []
while (n > 0):
r.append(n % 2)
n = n / 2
return r
def MillerRabin(n, s = 50):
for j in xrange(1, s + 1):
a = random.randint(1, n - 1)
b = toBinary(n - 1)
d = 1
for i in xrange(len(b) - 1, -1, -1):
x = d
d = (d * d) % n
if d == 1 and x != 1 and x != n - 1:
return True # Составное
if b[i] == 1:
d = (d * a) % n
if d != 1:
return True # Составное
return False # Простое
Ещё реализации:- http://en.literateprograms.org/Miller-Rabin_primality_test_%28Python%29
- http://code.activestate.com/recipes/410681-rabin-miller-probabilistic-prime-test/
- http://code.activestate.com/recipes/511459-miller-rabin-primality-test/
/^1?$|^(11+?)\1+$/Применять его следует не к самому целому числу. Вместо этого, нужно создать строку из единиц, где количество единиц соответствует самому числу и уже к этой строке применить регулярное выражение. Если совпадения нет — число простое. Так как же оно работает? Подвыражение (11+?) совпадает со строками вроде 11, 111, и т.д… Часть "\1+" будет искать далее по строке совпадения с результатами поиска первого подвыражения. В первый раз совпадение произойдет по строке «11» и потом поиск строки «11» будет произведен снова, а затем снова до конца строки. Если поиск завершится успешно, число не является простым. Почему? Потому, что будет доказано, что длина строки делится на 2 и, соответственно, само число тоже делится на два. Если совпадения не произойдет, движок регулярных выражений начнет искать строку «111» и ее повторения. Если первое подвыражение становится достаточно длинным (n/2) и совпадений по-прежнему не будет обнаружено, число будет являться простым.
Реализовывать я его не стал, не люблю регулярки(если кто напишет, жду в комменты, добавлю).
Используемая литература:


Комментариев нет:
Отправить комментарий