Раскраска графа

Рассмотрим математическую модель, используемую для управления
светофорами на сложном перекрестке дорог. Мы должны создать программу, которая в
качестве входных данных использует множество всех допустимых поворотов на перекрестке (продолжение прямой дороги, проходящей через перекресток, также будем
считать "поворотом") и разбивает это множество на несколько групп так, чтобы все повороты в группе могли выполняться одновременно, не создавая проблем друг для друга. Затем мы сопоставим с каждой группой поворотов соответствующий режим работы
светофоров на перекрестке.

*-Нравится статья? Кликни по рекламе! :)

Рис. 1.1. Сложный перекресток

Желательно минимизировать число разбиений исходного множества поворотов, поскольку при этом минимизируется количество режимов работы светофоров на перекрестке.
Для примера на рис. 1.1 показан перекресток возле Принстонского университета, известный сложностью его преодоления. Обратите внимание, что дороги С и E односторонние, остальные — двухсторонние. Всего на этом перекрестке возможно 13 поворотов. Некоторые-из этих поворотов, такие как АВ (поворот с дороги А на дорогу В) и ЕС, могут выполняться одновременно. Трассы других поворотов, например АО и ЕВ, пересекаются, поэтому их нельзя выполнять одновременно. Режимы работы светофоров должны учитывать эти обстоятельства.

Рис. 1.2. Граф, показывающий несо-
вместимые повороты

Для построения модели этой задачи можно применить математическую структуру, известную как граф. Для решения задачи можно нарисовать граф, где вершины будут представлять повороты, а ребра соединят ту часть вершин-поворотов, которые нельзя выполнить одновременно. Для нашего перекрестка соответствующий граф показан на рис. 1.2, а в табл. 1.1 дано другое представление графа — в виде таблицы(матрицы смежности), где на пересечении строки i и столбца j стоит 1 тогда и только тогда, когда существует ребро между вершинами i и j.

Таблица 1.1. Таблица несовместимых поворотов

В рамках этой модели можно использовать решение, которое дает математическая задача раскраски графа: каждой вершине графа надо так задать цвет, чтобы никакие две соединенные ребром вершины не имели одинаковый цвет, и при этом по возможности использовать минимальное количество цветов. При такой раскраске графа несовместимым поворотам будут окрашены в разные цвета.

Проблема раскраски графа изучается математиками уже несколько десятилетий, но теория алгоритмов мало что может сказать о решении этой проблемы. К сожалению, задача раскраски произвольного графа минимальным количеством цветов принадлежит классу задач, которые называются NP-полными задачами и для которых все известные решения относятся к типу "проверь все возможности" или "перебери все варианты". Для раскраски графа это означает, что сначала для  закраски вершин используется один цвет, затем — два цвета, потом — три и т.д., пока не будет получена подходящая раскраска вершин. В некоторых частных случаях можно предложить более быстрое решение, но в общем случае не существует
более эффективного (в значительной степени) алгоритма решения задачи раскраски, чем алгоритм полного перебора возможных вариантов.

Таким образом, поиск оптимального решения задачи раскраски графа требует больших вычислительных затрат. В этой ситуации можно воспользоваться одним из следующих трех подходов.

1. Если граф небольшой, можно попытаться найти оптимальное решение, перебрав все возможные варианты раскраски. Однако этот подход не приемлем для больших графов, так как программно трудно организовать эффективный перебор всех вариантов.
2. Второй подход предполагает использование дополнительной информации об исходной задаче. Желательно найти какие-то особые свойства графа, которые исключали бы необходимость полного перебора всех вариантов раскраски для нахождения оптимального решения.
3. В третьем подходе мы немного изменяем постановку задачи и ищем не оптимальное решение, а близкое к оптимальному. Если мы откажемся от требования минимального количества цветов раскраски графа, то можно построить алгоритмы раскраски, которые работают значительно быстрее, чем алгоритмы полного перебора.

Алгоритмы, которые быстро находят "подходящее", но не оптимальное решение, называются эвристическими.

 Примером рационального эвристического алгоритма может служить следующий "жадный" алгоритм раскраски графа. В этом алгоритме сначала мы пытаемся раскрасить как можно больше вершин в один цвет, затем закрашиваем во второй цвет также по возможности максимальное число оставшихся вершин, и т.д. При закраске вершин в новый цвет мы выполняем следующие действия.

1. Выбираем произвольную не закрашенную вершину и назначаем ей новый цвет.
2. Просматриваем список не закрашенных вершин и для каждой из них определяем, соединена ли она ребром с вершиной, уже закрашенной в новый цвет. Если
   не соединена, то к этой вершине также применяется новый цвет.

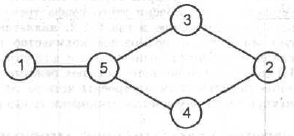Рис. 1.3. Граф

Этот алгоритм назван "жадным" из-за того, что каждый цвет применяется к максимально большому числу вершин, без возможности пропуска некоторых из них или перекраски ранее закрашенных. Возможны ситуации, когда, будь алгоритм менее "жадным" и пропустил бы некоторые вершины при закраске новым цветом, мы получили бы раскраску графа меньшим количеством цветов. Например, для раскраски графа на рис. 1.3 можно было бы применить два цвета, закрасив вершину 1 в красный цвет, а затем, пропустив вершину 2, закрасить в красный цвет вершины 3 и 4. Но "жадный" алгоритм, основываясь на порядковой очередности вершин(применив, например структуру Вирта, можно попытаться исправить это), закрасит в красный цвет вершины 1 и 2, для закраски остальных вершин потребуются еще два цвета.

Применим описанный алгоритм для закраски вершин графа нашей задачи (рис.1.2), при этом первой закрасим вершину АВ в синий цвет. Также можно закрасить в синий цвет вершины AC, AD и ВА, поскольку никакие из этих четырех вершин не имеют общих ребер. Вершину ВС нельзя закрасить в этот цвет, так как существует ребро между вершинами АВ и ВС. По этой же причине мы не можем закрасить в синий цвет вершины BD, DA и DB — все они имеют хотя бы по одному ребру, связывающему их с уже закрашенными в синий цвет вершинами. И так, продолжая перебор, закрашиваем все возможные вершины. Теперь применим второй цвет, например красный и повторим всё заново.

Таблица 1.2. Раскраска графа, представленного на рис. 1.2

Назначенные вершинам цвета приведены в табл. 1.2. В этой таблице "дополнительные" повороты совместимы с соответствующими поворотами из столбца "Повороты", хотя алгоритмом они окрашены в разные цвета. При задании режимов работы светофоров, основанных на одном из цветов раскраски, вполне безопасно включить в эти режимы
и дополнительные повороты.

Можно использовать результаты из общей теории графов для оценки качества полученного решения. В теории графов k-кликой называется множество из k вершин, в котором каждая пара вершин соединена ребром. Очевидно, что для закраски k-клики необходимо k цветов, поскольку в клике никакие две вершины не могут иметь одинаковый цвет.

B графе рис. 1.2 множество из четырех вершин AC, DA, BD и ЕВ является 4-кликой.
Поэтому,  не существует раскраски этого графа тремя и менее цветами, и,
следовательно, (решение, представленное в табл. 1.2 является оптимальным в том
смысле, что использует минимально возможное количество цветов. В терминах исходной задачи это означает, что для управления перекрестком, показанным на рис; 1.1, необходимо не менее четырех режимов работы светофора.

Теперь привожу реализацию алгоритма, результат которого полностью совпадает с таблицей 1.2!

     # ab ac ad ba bc bd da db dc ea eb ec ed
N =  [[0,0,0,0,1,1,1,0,0,1,0,0,0],# ab
     [0,0,0,0,0,1,1,1,0,1,1,0,0], # ac
     [0,0,0,0,0,0,0,0,0,1,1,1,0], # ad
     [0,0,0,0,0,0,0,0,0,0,0,0,0], # ba
     [1,0,0,0,0,0,0,1,0,0,1,0,0], # bc
     [1,1,0,0,0,0,1,0,0,0,1,1,0], # bd
     [1,1,0,0,0,1,0,0,0,0,1,1,0], # da
     [0,1,0,0,1,0,0,0,0,0,0,1,0], # db
     [0,0,0,0,0,0,0,0,0,0,0,0,0], # dc
     [1,1,1,0,0,0,0,0,0,0,0,0,0], # ea
     [0,1,1,0,1,1,1,0,0,0,0,0,0], # eb
     [0,0,1,0,0,1,1,1,0,0,0,0,0], # ec
     [0,0,0,0,0,0,0,0,0,0,0,0,0]] # ed

#раскраска графа
def graphColoring():
    colored=[[]]
    color=0#№ цвета
    stack=[]#покрашенные узлы
    num2=num1=-1
#функция проверки возможности покраски в используемый сейчас цвет
    def loop(num):
        for t in colored[color]:
            if N[t][num]==1:
                return False
        return True
    
    for a in N:
        num1+=1
        if num1 not in stack:#просматриваем только те, которые еще не покрашены
            if not loop(num1):#значит применяем новый цвет
                colored.append([])
                color+=1
                stack.append(num1)
                colored[color].append(num1)
            num2=num1
            for b in a[num1:]:
                if b==0 and num2 not in stack and loop(num2):
                    stack.append(num2)
                    colored[color].append(num2)  
                num2+=1
    return colored

Подставьте теперь новый граф, на примере которого объяснялась жадность алгоритма и вы увидите доказательство тому.

Думая, по дороге на работу, над тем, как избавиться от жадности алгоритма, я пришёл к следующей идее. А что если нам проходиться начиная с узла максимальной мощности(больше всего связей), окрашивать его и переходить к соседу, так же с макс. мощностью, окрашивая в другой цвет и проверяя в стеке цвета(если их уже окрасили) других своих соседей. Реализацию данной идее вы можите лицезреть в самом низу, под названием VirtGraphColoring2(рекурсивная реализация). Потом я подумал, а почему бы не разработать теорию максимезации энтропии(мощности) узлов графа. Эта идея была навеяна прошлым алгоритмом и стратегическими играми, ну знаете, когда от склада с оружием зависят разные точки и разрушив его мы избавляемся, фактически, и от них. И я не стал следовать к соседу с макс. мощностью, а просто прошёлся по узлам в порядке убывания их мощностей, раскрашивая в разные цвета. Радует, что пока что я не нашёл такого графа, который бы они раскрасили не оптимально))) Просьба, подкинуть!))

Edges = {'1':['8', '5', '6'], '2':['6','7', '9'], '3':['7', '10', '5'], '4':['8','10', '9'], '9':['4','5', '2'], '10':['3', '4', '6'], '5':['1', '9', '3'], '6':['1', '2', '10'], '7':['8', '2', '3'], '8':['7', '1', '4']}

#функция раскраски в порядке мощностей узлов
def VirtGraphColoring(Edges):
    result={}
    colors=[0]
  
    def SortEdges():
        sort={}
        for key in Edges:
            sort[key]=len(Edges[key])
        sort2=sorted(sort.iteritems(), key=lambda (k,v):(v,k), reverse=True)
        return sort2
    
    def colorize():
        def removeColor():
            for color in colors:
                if color not in stackColor: return color
            color=colors[-1]+1
            colors.append(color)
            return color
    
        for key in sort:
            stackColor=[]
            for key2 in Edges[key[0]]:
                if key2 in result:stackColor.append(result[key2])
            color=removeColor()
            result[key[0]]=color
        return result
    
    sort=SortEdges()
    return colorize()

print VirtGraphColoring(Edges)

#рекурсивная функция раскраски в порядке мощностей соседей
def VirtGraphColoring2(Edges):
    result={}# результат
    colors=[0]#стек использованных цветов
    sort1={}# ссловарь ключей с их мощностью(количеством соседей)
  
    def SortEdges(): # сортируем словарь
        for key in Edges:
            sort1[key]=len(Edges[key])
        sort2=sorted(sort1.iteritems(), key=lambda (k,v):(v,k), reverse=True)
        return sort2 # список упорядоченных по мощности кортежей вида (ключ, мощность)
    
    def colorize(key):
        def removeColor(): #возвращает нужный цвет 
            for color in colors:
                if color not in stackColor: return color #если можне выбрать цвет, используемый ранее
            color=colors[-1]+1 # нет, тогда новый цвет
            colors.append(color) # добавляем его в коллекцию
            return color
        
        stackColor=[]
        maxi=-1
        maxkey=None
        for key2 in Edges[key]:
            if key2 not in result and sort1[key2]>maxi: 
                maxi=sort1[key2]
                maxkey=key2
            if key2 in result:stackColor.append(result[key2])
        color=removeColor()
        result[key]=color
        sort.remove((key,sort1[key]))
        if maxkey != None: colorize(maxkey)
        elif len(sort)>0: colorize(sort[0][0])

    sort=SortEdges()
    colorize(sort[0][0])   
    return result   

Тут обнаружил, что задача раскраски графа, это решение судоку)) Вот так игры и создаются))