Под топологической сортировкой понимается сортировка элементов, для которых определен частичный порядок, т.е. упорядочивание задано не для всех, а только для некоторых пар элементов.
Задача топологической сортировки графа состоит в следующем: указать такой линейный порядок на его вершинах, чтобы любое ребро вело от вершины с меньшим номером к вершине с большим номером. Очевидно, что если в графе есть циклы, то такого порядка не существует.
*-Нравится статья? Кликни по рекламе! :)
Существует несколько способов топологической сортировки — из наиболее известных:
- Алгоритм Демукрона
- Метод сортировки для представления графа в виде нескольких уровней
- Метод топологической сортировки с помощью обхода в глубину
Алгоритм с помощью обхода в глубину
Суть алгоритма
Поиск в глубину или обход в глубину (англ. Depth-first search, сокращенно DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.Запускаем обход в глубину, и когда вершина обработана, заносим ее в стек. По окончании обхода в глубину вершины достаются из стека. Новые номера присваиваются в порядке вытаскивания из стека.
Цвет: во время обхода в глубину используется 3 цвета. Изначально все вершины белые. Когда вершина обнаружена, красим ее в серый цвет. Когда просмотрен список всех смежных с ней вершин, красим ее в черный цвет.
Думаю будет проще рассмотреть данный алгоритм на примере:
Имеем бесконтурный ориентированный граф.
Изначально все вершины белые, а стек пуст.
Начнем обход в глубину с вершины номер 1.
↑ Переходим к вершине номер 1. Красим ее в серый цвет.
↑ Существует ребро из вершины номер 1 в вершину номер 4. Переходим к вершине номер 4 и красим ее в серый цвет.
↑ Существует ребро из вершины номер 4 в вершину номер 2. Переходим к вершине номер 2 и красим ее в серый цвет.
↑ Из вершины номер 2 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 2 в черный цвет и кладем ее в стек.
↑ Существует ребро из вершины номер 4 в вершину номер 3. Переходим к вершине номер 3 и красим ее в серый цвет.
↑ Из вершины номер 3 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 4. Красим вершину номер 3 в черный цвет и кладем ее в стек.
↑ Из вершины номер 4 нет рёбер, идущих не в черные вершины. Возвращаемся к вершине номер 1. Красим вершину номер 4 в черный цвет и кладем ее в стек.
↑ Из вершины номер 1 нет рёбер, идущих не в черные вершины. Красим её в черный цвет и кладем в стек. Обход точек закончен.
↑ По очереди достаем все вершины из стека и присваиваем им номера 1, 2, 3, 4 соответсвенно. Алгоритм топологической сортировки завершен. Граф отсортирован.
И всем бы это объяснение было хорошо, если бы не одно НО:
Если мы начнем сортировку с 4-го элемента, то никогда не вернемся в 1-й, т.к. мы в нём еще не были, а из 4-го в 1-й стрелочки не идет) Эта проблема полностью ложится на внутреннюю реализацию алгоритма. Я ввел переменную path=[] дабы отслеживать путь перемещения по графу. Т.е. при переходе к новому эл-ту я ддобавляю его в path, а при возвращении - удаляю. Таким образом, нам останется проверить в момент опустения path все ли эл-ты мы прошли и если нет, то запустить алгоритм для любой из еще не просмотренных элементов.
Я использовал здесь матрицы смежности, т.к. считаю, что разрабатывать алгоритм проще, начиная именно с такого представления графа, а уже после вводить необходимые структуры данных.
Например в данной реализации, я делаю N2 проверок связи узлов, в то время, как введя, например, связный список, для точной связи элементов, можно избавиться от if вообще и останется N конкретных действий.
Важно!
Циклы в графе есть тогда и только тогда, когда при обходе в глубину мы 'уткнемся' в свой 'серый хвост'.
roofs=['a', 'b', 'c', 'd', 't']
matrix = {('a', 'c'):1, ('c', 'b'):1, ('d', 'b'):1, ('d', 'c'):1, ('d', 't'):1}
#топологическая сортировка поиском в глубину
def topologicSortDFS(v, roof, firstNode=0):
path=dict()#для разделения несвязных элементов графа
result=[]#стек результата
length=len(roof)
global col
col=0
def topologicSort(v, roof, firstNode=0):
global col
path[roof[firstNode]]=1
col+=1
for i in range(length):
if roof[i] not in result and v.get((roof[firstNode],roof[i]),0)==1:
if path.get(roof[i],0)==1:
print "!!!имеется цикл!!!"
exit()
topologicSort(v,roof,i)
if i==length-1:
result.append(roof[firstNode])
col-=1
if col==0 and len(result)!=length:#для отслеживания несвязанных участков
for x in roof:
if x not in result:topologicSort(v,roof, roof.index(x))
return result#номер для занесения в стек
return topologicSort(v, roof, firstNode)
Я ничего не раскрашиваю тут, а использую фактически 2 стека, но увы эта моя реализация не смогла превзойти классическую функцию, которую я привожу ниже.
#Color — массив, в котором хранятся цвета вершин (0 — белый, 1 — серый, 2 — черный).
#Edges — массив списков смежных вершин.
#Numbers — массив, в котором сохраняются новые номера вершин.
#Stack — стек, в котором складываются вершины после их обработки.
#Cycle — принимает значение true, если в графе найден цикл.
Edges = {'a':['c'], 'c':['b'], 'd':['c', 'b', 't'], 'b':[], 't':[]}
def topologicSortDFS2(Edges):
Stack=[]
Color=dict()
for i in Edges.keys():
Color[i]=0
def topological_sort():
def dfs(v):
#Если вершина серая, то мы обнаружили цикл.
#Заканчиваем поиск в глубину.
if Color[v] == 1: return True
if Color[v] == 2: return False#Если вершина черная, то заканчиваем ее обработку.
Color[v] = 1#Красим вершину в серый цвет.
#Обрабатываем список смежных с ней вершин.
for i in range(len(Edges[v])-1):
if dfs(Edges[v][i]): return True
Stack.append(v)#Кладем вершину в стек.
Color[v] = 2#Красим вершину в черный цвет.
return False;
#Вызывается обход в глубину от всех вершин.
#Заканчиваем работу алгоритма, если обнаружен цикл.
for i in Edges.keys():
Cycle = dfs(i)
if Cycle:
print "!!!имеется цикл!!!"
exit()
#Заносим в массив новые номера вершин.
Stack.reverse()
return Stack
return topological_sort()
Результаты тестов приведу в конце!)Алгоритм представления графа в виде уровней
Пусть дан бесконтурный ориентированный простой граф G = (V,E).Через
обозначим множество вершин таких, что 
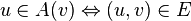.То есть, A(v) — множество всех вершин, из которых есть ребро в вершину v.
Пусть P — искомая последовательность вершин.
Наличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину v.пока | P | < | V | выбрать любую вершину v такую, чтои
удалить v из всех
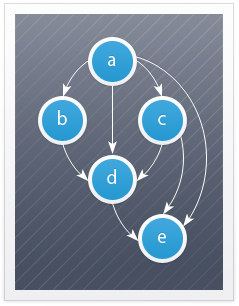
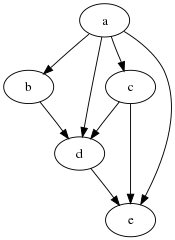
Пример работы алгоритма
.В таком случае алгоритм выполнится следующим образом:
| шаг | v | A(a) | A(b) | A(c) | A(d) | A(e) | P |
|---|---|---|---|---|---|---|---|
| 0 | - |  | a | a | a,b,c | a,c,d | |
| 1 | a | | | | b,c | c,d | a |
| 2 | c | | | | b | d | a,c |
| 3 | b | | | | | d | a,c,b |
| 4 | d | | | | | | a,c,b,d |
| 5 | e | | | | | | a,c,b,d,e |
На втором шаге вместо c может быть выбрана вершина b, поскольку порядок между b и c не задан.
Рассмотрим более подробно.
Каждую вершину можно охарактеризовать числом дуг, входящих в неё (полустепень захода), и числом дуг, исходящих из неё к другим вершинам (полустепень исхода).
Если у вершины нет ни одной входящей дуги, вершина называется источником сети.
Если у вершины нет ни одной исходящей дуги, вершина называется стоком сети.
Сначала опишем, что же мы хотим от нашего алгоритма, а потом приведем код.
Итак, наша цель — создать сеть, состоящую из нескольких уровней.
Из рисунка видно, что задачи внутри одного уровня зависят только от задач на младших уровнях, и независимы друг от друга.
В таком случае, для достижения цели нам сначала надо в любом порядке выполнить все задачи уровня 0, потом, в любом порядке, задачи уровня 1, и т.д., до уровня 3 (последнего).
Для решения задачи, нам понадобится представление графа в виде матрицы (ij элемент = 1, если есть дуга из вершины i в вершину j, и равен 0, если дуги нет).
В строке под таблицей даны полустепени захода для всех вершин. Каждое число отражает сумму единичек в соответствующем столбце матрицы.
На первом шаге алгоритма мы выбираем все вершины с нулевой полустепенью захода, заносим их в нулевой уровень и, мысленно, выкидываем из графа.
В результате, (мы больше не учитываем строки матрицы, соответствующие обработанным вершинам) полустепени захода остальных вершин уменьшатся.
Далее, проделываем тоже самое с оставшимися вершинами, имеющими нулевую полустепень захода и помещаем их в первый уровень:
Последующие шаги выполняются аналогично!
Приведем код реализации, за пример взяв прошлый граф.
#топологическая сортировка уровнями
class Graph:
def __init__(self):
self.nodes=[[0,0,0,0,0,0],
[1,0,0,1,0,0],
[0,1,0,1,0,0],
[0,0,0,0,0,0],
[0,0,0,1,0,0]
];
self.count=range(len(self.nodes))
def GetInputNodesArray(self):
array = []
for i in self.count:
step=0
for j in self.count:
if self.nodes[i][j]==1:step+=1
array.insert(i,step)
return array;
def TopologicSort(self):
levels =[];
workArray = self.GetInputNodesArray();
completedCounter = 0;
currentLevel = 0;
while (completedCounter != len(self.nodes)):
for i in self.count:
if (workArray[i] == 0):
ind=0
#добавляем обработанную вершину
levels.insert(completedCounter,i);
for node in self.nodes:
if node[i]==1:
workArray[ind]-=1
ind+=1
workArray[i] = -1; # Помечаем вершину как обработанную
completedCounter+=1;
currentLevel+=1;
levels.reverse()
return levels#осталось выбрать в обратном порядке
Данный метод, от 2-х предыдущих примеров отличает то, что используется больше памяти на входе, т.к. мы описываем связь каждого узла с каждым. В предыдущем же алгоритме мы хранили только связи с соседями! Насколько оправдано это, смотри в конце статьи в результатах тестов!)Топологическая сортировка графа в виде структуры Вирта.
Еще 1 пример сортировки уровнями, но в другой структуре.
О самой структуре Вирта, я писал раньше, в статье "Теория графов и деревьев для Python"
Поэтому перейду сразу к описанию алгоритма.
Для данного графа Edges = {'1':['2','4'], '2':['8'], '4':['8'], '5':['8'], '8':[]}
Рис.1. Структура Вирта
После оптимизации, в нашем случае, структура видоизменится следующим образом:
Рис.2. Результат оптимизации
def VirtTopSort():
result=[]
z=len(Edges)
head=ceateVirtStructLeader(Edges)
#Оптимизация
#Поиск ведущих с нулевым количеством предшественников.
p=head
head=None
while p!=None:
q=p
p=p.Next
if q.Count==0:
q.Next=head
head=q
q = head
while q!=None:
#счетчик z для подсчета ведущих узлов
#он должен вновь стать равным нулю в конце работы программы
#или имеем цикл!
z-=1
#Занести элемент в результат и исключить его.
result.append(q.Key)
t=q.Trail
q=q.Next
while t!=None:
# Уменьшить счетчик предшественников у всех его
# последователей в списке ведомых t; если какой-
#либо счетчик стал равен 0, то добавить этот
# элемент к списку ведущих q;
# p - вспомогательная переменная, указывающая на
# ведущий узел, счетчик которого нужно уменьшить
# и проверить на равенство нулю.
p=t.Id
p.Count-=1
if p.Count==0: #Включение p в список ведущих.
p.Next = q;
q = p;
t = t.Next;
if z!=0:
print "цикл!!!"
exit()
result.reverse()
return result
В зарубежном интернете нашел еще один алгоритм, решил привести его здесь, для полноты картины!
Алгоритм R. E. Tarjan от 1972 года
Алгоритм является модификацией алгоритма с применением обхода в глубину
#Алгоритм R. E. Tarjan от 1972 года
def topological_sort(items, partial_order):
def add_node(graph, node):
"""Добавить узел в графе если он еще не существует."""
if not graph.has_key(node):
graph[node] = [0] # 0 = число дуг входящих в этот узел.
def add_arc(graph, fromnode, tonode):
"""Добавить дуги графа.
Можно создать несколько дуг.
Конечные узлы должны уже существовать."""
graph[fromnode].append(tonode)
# Обновление количество входящих дуг в узле.
graph[tonode][0] = graph[tonode][0] + 1
# Шаг 1 - создание ориентированного графа с дугой b-->a для каждого входа
# Паре (a, b).
# Граф представлен словарём.Словарь содержит:
# Пару item:list для каждого узла в графе. /item/ это значение узла
# /list/ с первым пунктом является счетчиком входящих дуг, а
# остальные направления исходящих дуг. Например:
# {'a':[0,'b','c'], 'b':[1], 'c':[1]}
# получим следующий граф: c <-- a --> b
graph = {}
for v in items:
add_node(graph, v)
for a,b in partial_order:
add_arc(graph, a, b)
# Шаг 2 - найти все корни (узлы с нулевым входящих дуг).
roots = [node for (node,nodeinfo) in graph.items() if nodeinfo[0] == 0]
# Шаг 3 - неоднократно выделяют корень и удаляем его из графа.
# Удаление узла может преобразовывать некоторые из прямых потомков узла в корни.
# Всякий раз, когда это произойдет, мы добавляем новые корни в список корней
sorted = []
while len(roots) != 0:
# Если длина (roots) всегда равна 1, когда мы сюда попали, это означает, что
# вход описывает законченый порядок, и есть только
# один возможный вывод.
# Когда длина (roots)> 1, мы можем выбрать любой корень, чтобы отправить
# на выход; эта свобода представляет несколько полной упорядоченности
# Мы произвольно принимать один из
# корней использованием pop(). Заметим, что для алгоритма, чтобы быть эффективным,
# эта операция должна быть сделана за O(1) времени.
root = roots.pop()
sorted.append(root)
for child in graph[root][1:]:
graph[child][0] = graph[child][0] - 1
if graph[child][0] == 0:
roots.append(child)
del graph[root]
if len(graph.items()) != 0:
# Существует цикл!
print "цикл!!!"
exit()
return sorted
print topological_sort(['a','b','c','d','t'], [('t','d'),('b','d'),('c','d'),('b','c'),('c','a')])
Примеры использования топологической сортировки
Техническая задача разбивается на ряд подзадач, при этом выполнение одних подзадач должно предшествовать выполнению других подзадач. Топологическая сортировка означает выполнение подзадач в таком порядке, чтобы перед началом выполнения каждой подзадачи все необходимые для этого подзадачи были уже выполнены.
В программе некоторые процедуры могут вызывать другие процедуры. Топологическая сортировка предполагает расположение описаний процедур в таком порядке, чтобы вызываемые процедуры описывались раньше тех, которые их вызывают. Сборка приложения
Дуга, идущая из вершины «Код» в вершину «Результирующий файл» говорит о том, что «Код» должен быть обработан прежде, чем будет получен Result.exe
Перед тем, как вершина может быть обработана, следует обработать все вершины, ссылающиеся на неё.
При помощи топологической сортировки строится корректная последовательность выполнения действий, всякое из которых может зависеть от другого: последовательность прохождения учебных курсов студентами, установки программ при помощи пакетного менеджера, сборки исходных текстов программ при помощи Makefile'ов.
При распараллеливании алгоритмов, когда по некоторому описанию алгоритма нужно составить граф зависимостей его операций и, отсортировав его топологически, определить, какие из операций являются независимыми и могут выполняться параллельно (одновременно).
Примером использования топологической сортировки может служить создание карты сайта, где имеет место древовидная система разделов.
Результаты тестов
Тест проводился путем исполнения 10000 раз определенной функции в profile с использованием функции test.
Мой самодельный алгоритм.
profile.run('test(topologicSortDFS2, 10000, Edges)')
420005 function calls (380005 primitive calls) in 4.598 seconds
Я думаю улучшить его, разбивая на подграфы, но много ли это принесет, увидим позже.
Классический алгоритм поиска в глубину и раскраски.
profile.run('test(topologicSortDFS, 10000, matrix, roofs)')
270005 function calls (250005 primitive calls) in 2.915 seconds
Алгоритм разбиения уровнями, с представлением графа в виде матрицы смежности
profile.run('test(gr.TopologicSort,10000)')
160005 function calls in 1.688 seconds
С алгоритмом использующим структуру Вирта, Всё несколько интереснее.
profile.run('test(VirtTopSort,10000)')
Скорость его выполнения
780005 function calls (750005 primitive calls) in 8.322 seconds
из них 10000 1.227 0.000 6.676 0.001 __init__.py:150(ceateVirtStructLeader)
Уходит на создание самой структуры! Т.е. фактическое время исполнения метода около 1.5 сек, но использовать его нужно там, где используется данная структура сразу, а несоздается специально для данной функции!
Ну и в заключение алгоритм R. E. Tarjan от 1972 года
profile.run("test(topological_sort,10000,['a','b','c','d','t'], [('t','d'),('b','d'),('c','d'),('b','c'),('c','a')])")
430005 function calls in 3.901 seconds
Хоть он и считается модифицированной версией алгоритма номер 2, но почему то он проиграл ему секунду! Может я просто нашел плохую его реализацию?
Используемая литература:
topologicSortDFS2 не работает!
ОтветитьУдалитьinput
{'NZVS': ['ORE'], 'DCFZ': ['ORE'], 'FUEL': ['XJWVT', 'KHKGT', 'QDVJ', 'NZVS', 'GPVTF', 'HKGWZ'], 'QDVJ': ['HKGWZ', 'GPVTF', 'PSHF'], 'PSHF': ['ORE'], 'HKGWZ': ['ORE'], 'XJWVT': ['DCFZ', 'PSHF'], 'GPVTF': ['ORE'], 'KHKGT': ['DCFZ', 'NZVS', 'HKGWZ', 'PSHF']}
output
['PSHF', 'FUEL', 'QDVJ', 'GPVTF', 'KHKGT', 'HKGWZ', 'XJWVT', 'DCFZ', 'NZVS']
expected
['FUEL', 'XJWVT', 'QDVJ', 'KHKGT', 'PSHF', 'HKGWZ', 'NZVS', 'DCFZ', 'GPVTF', 'ORE']
Я не мог поверить, что существует настоящий онлайн-кредитор, который может быть таким добрым и честным, как Бенджамин Ли, который предоставил мне ссуду в 2 миллиона евро для выполнения моего проекта, который так долго ждал своего исполнения, но с С помощью офицера Бенджамина все было легко для меня. Я скажу вам связаться с кредитным офицером Бенджамином Ли по адресу 247officedept@gmail.com
ОтветитьУдалитьне благодари
ОтветитьУдалить