Теория графов и деревьев для Python

 Многие задачи, например, задача обхода точек по кратчайшему маршруту, могут быть решены с помощью одного из мощнейших инструментов — с помощью графов. Часто, если вы можете определить, что решаете задачу на графы, вы по-крайней мере на полпути к решению. А если ваши данные можно каким-либо образом представить как деревья, у вас есть все шансы построить действительно эффективное решение.
Графами можно представить любую структуру или систему, от транспортной сети до сети передачи данных и от взаимодействия белков в ядре клетки до связей между людьми в Интернете.
*-Нравится статья? Кликни по рекламе! :)
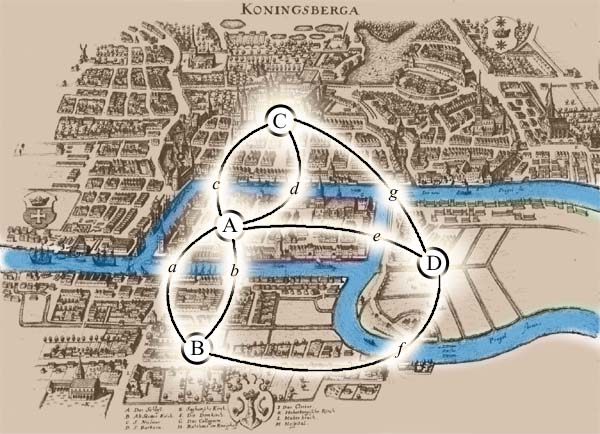
Зарождением теории графов можно считать решение проблемы семи мостов Кёнигсберга,
изображенной на картинке под заголовком статьи.

Графы могут стать еще полезнее, если добавить в них дополнительные данные вроде весов или расстояний, что даст возможность описывать такие разнообразные проблемы как игру в шахматы или определение подходящей работы для человека в соответствии с его способностями.
Деревья — это просто особый вид графов, так что большинство алгоритмов и представлений графов сработают и для них.
Однако, из-за их особых свойств (связность и отсутствие циклов), можно применить специальные (и весьма простые) версии алгоритмов и представлений.
На практике в некоторых случаях встречаются структуры (такие как XML-документы или иерархия каталогов), которые могут быть представлены в виде деревьев (с учетом атрибутов IDREF и символьных ссылок XML-документы и иерархия каталогов становятся собственно графами). На самом деле эти «некоторые» случаи довольно-таки общие.

Описание задачи в терминах графов является довольно абстрактным, так что если вам нужно реализовать решение, вы должны представить графы в виде каких-либо структур данных. (Это придется делать даже при проектировании алгоритма и только, потому что нужно знать, сколько времени будут выполняться различные операции на представлении графа). В некоторых случаях граф будет уже составлен в коде или данных, так что отдельной структуры не потребуется. Например, если вы пишете веб-краулер, собирающий информацию о сайтах по ссылкам, графом будет сама сеть. Если у вас есть класс Person с атрибутом friends, являющимся списком других объектов типа Person, то ваша объектная модель уже будет графом, на котором можно использовать различные алгоритмы. Однако существуют и специальные способы представления графов.

В общих словах, мы ищем способ реализации функции смежности, N(v), так, чтобы N[v] было каким-либо набором (или в отдельных случаях просто итератором) смежных с v вершин. Как и во многих других книгах мы сосредоточимся на двух наиболее известных представлениях: списках смежности и матрицах смежности, потому что они наиболее полезны и обобщены. Альтернативные представления описаны в последнем разделе ниже.

«Черный ящик»: словари и множества

Существует техника, подробно описываемая в большинстве книг 

об алгоритмах, и неявно используемая программистами на Python, 

это — хэширование. 

Хэширование подразумевает вычисление целого числа 

часто выглядящего как случайное), основанного на произвольном объекте.

Потом это значение можно будет использовать, например, как индекс

в массиве (после некоторых преобразований, чтобы не выйти за границы 

массива).

Стандартный механизм хэширования в Python представлен функцией hash:
>>> hash(42)
42
>>> hash("Hello, world!")
-1886531940
Этот механизм используется в словарях, реализованных как так 

называемыехэш-таблицы. Множества реализованы тем же способом. 

Важная особенность в том, что хэш может быть вычислен по существу 

за константное время (оно постоянно относительно размера хэш-таблицы, 

но линейно зависит от размера хэшируемого объекта). Если существует 

достаточно большой массив, то доступ к нему с помощью хэша в среднем 

занимает Θ(1). (В худшем случае это займет Θ(n), если только мы не знаем 

значений заранее и не напишем собственную хэш-функцию. Но в любом случае, 

на практике хэширование очень эффективно). 

Для нас это значит, что доступ к элементам в dict или set происходит за постоянное 

время, а это делает их в высшей степени полезными строительными блоками для более 

сложных структур и алгоритмов.

Списки смежности и тому подобное

Один из наиболее очевидных способов представления графов — это списки смежности. Смысл их в том, что для каждой вершины создается список (или множество, или другой контейнер или итератор) смежных с ней вершин. Разберем простейший способ реализации такого списка, предположив, что имеется n вершин, пронумерованных 0… n-1.

Само собой, вершины могут быть представлены любыми объектами и иметь 

собственные метки или имена. Однако использование целых чисел в 

диапазоне 0… n-1 делает реализацию многих представлений проще, 

потому что в таком случае номера вершин можно использовать как индексы.

Таким образом, каждый список смежности является списком таких номеров, а сами эти списки собраны в главный список размера n, индексированный номерами вершин. Обычно сортировка таких списков случайная, так что речь в действительности идет об использовании списков для реализации множеств смежности. Термин список просто исторически устоялся. Python, к счастью, имеет отдельный тип для множеств, который во многих случаев удобно использовать.

Примерный граф, для которого будут показаны разные представления, изображен на рис. 1. Для начала положим, что все вершины пронумерованы (a=0, b =1, …). С учетом этого граф можно представить очевидным способом, как показано в следующем листинге. Чтобы было удобнее, я присвоил номера вершин переменным, названным в соответствии с метками вершин на рисунке. Но можно работать и прямо с числами. Какой вершине какой список принадлежит указано в комментариях. Если хотите, потратьте несколько минут, чтобы убедиться, что представление соответствует рисунку.

a, b, c, d, e, f, g, h = range(8)
N = [
 {b, c, d, e, f}, # a
 {c, e}, # b
 {d}, # c
 {e}, # d
 {f}, # e
 {c, g, h}, # f
 {f, h}, # g
 {f, g} # h
]

В версиях Python до 2.7 (или 3.0) нужно описывать множества как 

set([1, 2, 3]) вместо {1, 2, 3}. Но пустое множество в новых версиях 

по-прежнему записывается как set(), потому что {} объявляет пустой словарь.

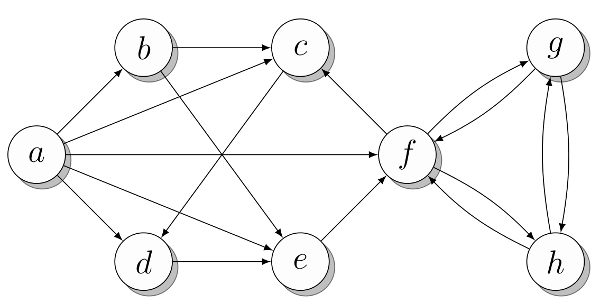
Рис. 1. Примерный граф для демонстрации разных видов представления

Имя N из листинга связано с функцией N, описанной выше. В теории графов N(v) представляет множество смежных с v вершин. Так же и в нашем коде N[v] является множеством смежных с v вершин. Предполагая, что N определена как в примере выше, в интерактивном режиме Python можно поизучать это представление:

>>> b in N[a]  # смежная?
True
>>> len(N[f])  # степень
3

Другим возможным представлением, которое в некоторых случаях даст меньше накладных расходов, являются собственно списки смежности. Пример такого списка приведен в листинге ниже. Доступны все те же операции, но проверка смежности вершины выполняется за Θ(n). Это дает серьезное снижение скорости, но если вам действительно требуется это представление, то это его единственная проблема. (Если все, что делает ваш алгоритм — это обход соседних вершин, то использование объектов типа множество не просто бессмысленно: накладные расходы могут ухудшить постоянные множители в асимптотике вашей реализации).

a, b, c, d, e, f, g, h = range(8)
N = [
 [b, c, d, e, f], # a
 [c, e], # b
 [d], # c
 [e], # d
 [f], # e
 [c, g, h], # f
 [f, h], # g
 [f, g] # h
]

Можно поспорить, что это представление на самом деле — набор массивов смежности, а не классические списки смежности, т.к. тип список в Python в действительности является динамическим массивом. Если хотите, вы можете реализовать тип связанного списка и использовать его вместо типа list из Python. Это может сделать дешевле в плане производительности произвольные вставки в список, но вам, вероятно, и не понадобится такая операция, потому что с тем же успехом можно добавлять новые вершины к концу списка. Преимущество использования встроенного list в том, что он представляет собой очень быструю и хорошо отлаженную структуру (в отличие от любых структур списков, которые можно реализовать на чистом Python).

При работе с графами постоянно всплывает идея о том, что лучшее представление зависит от того, что именно нужно сделать с графом. Например, используя списки (или массивы) смежности можно сохранить накладные расходы небольшими и обеспечить эффективный обход N(v) для любой вершины v. Однако, проверка, являются ли u и v смежными, потребует времени Θ(N(v)), что может стать проблемой при высокой плотности графа (т.е. при большом числе ребер). В этих случаях на помощь придут множества смежности.

Совет:
Известно, что удаление объектов из середины list в Python довольно затратно. Удаление с конца при этом происходит за константное время. Если вы не заботитесь о порядке вершин, то можете удалять случайную вершину за константное время перезаписывая ее той, что находится в конце списка смежности, и вызывая затем метод pop.

Небольшой вариацией на тему этого представления можно назвать сортированные списки смежных вершин. Если списки нечасто меняются, их можно держать отсортированными и использовать бисекцию для проверки смежности вершины, что приведет к немного меньшим накладным расходам (в плане использования памяти и времени итерации), но увеличит сложность проверки до Θ(log₂ k), где k — количество смежных с данной вершин. (Это все равно очень маленькое значение. На практике, впрочем, использование встроенного типа set доставляет гораздо меньше хлопот).

Еще одна небольшая доработка заключается в использовании словарей вместо множеств или списков. Смежные вершины могут быть ключам словаря, а в качестве значения можно использовать любые дополнительные данные, например, вес ребра. Как это выглядит можно увидеть в листинге ниже (веса выбраны случайно).

a, b, c, d, e, f, g, h = range(8)
N = [
 {b:2, c:1, d:3, e:9, f:4},# a
 {c:4, e:3}, # b
 {d:8}, # c
 {e:7}, # d
 {f:5}, # e
 {c:2, g:2, h:2}, # f
 {f:1, h:6}, # g
 {f:9, g:8} # h
]

Словарь смежности можно использовать точно так же как и другие представления, с учетом дополнительной информации о весах:

>>> b in N[a] # смежность
True
>>> len(N[f]) # степень
3
>>> N[a][b]  # вес (a, b)
2

Если хотите, можете использовать словари смежности даже если у вас нет полезных данных вроде весов ребер (используя None или другое значение вместо данных). Это даст вам все преимущества множеств смежности, но при этом будет работать с (очень-очень) старыми версиями Python, не имеющими поддержки типа set(множества были введены в Python 2.3 в виде модуля sets. Встроенный тип set доступен начиная с Python 2.4).

До этого момента сущность, хранящая структуры смежности — списки, множества или словари — была списком, индексированным номерами вершин. Более гибкий вариант (позволяющий использовать произвольные, хэшируемые, имена вершин) строится на базе словаря в качестве основной структуры (такие словари со списками смежности Гвидо ван Россум использовал в своей статье «Python Patterns — Implementing Graphs», выложенной по адресу www.python.org/doc/essays/graphs.html). Листинг ниже показывает пример словаря, содержащего множества смежности. Заметьте, что вершины в нем обозначены символами.

N = {
 'a': set('bcdef'),
 'b': set('ce'),
 'c': set('d'),
 'd': set('e'),
 'e': set('f'),
 'f': set('cgh'),
 'g': set('fh'),
 'h': set('fg')
}

Если из листинга выше выбросить конструктор set, то останутся строки смежности, которые будут работать как списки смежности (неизменяемые) из символов (с чуть меньшими накладными расходами). Казалось бы, далеко не лучшее представление, но, как и было сказано выше, все зависит от вашей программы. Откуда вы получаете данные для графа? (Может быть, они уже в виде текста?) Как вы собираетесь их использовать?

Матрицы смежности

Другая распространенная форма представления графов — это матрицы смежности. Основное отличие их в следующем: вместо перечисления всех смежных с каждой из вершин, мы записываем один ряд значений (массив), каждое из которых соответствует возможной смежной вершине (есть хотя бы одна такая для каждой вершины графа), и сохраняем значение (в виде True или False), показывающее, действительно ли вершина является смежной. И вновь простейшую реализацию можно получить используя вложенные списки, как видно из листинга ниже. Обратите внимание, что это также требует, чтобы вершины были пронумерованы от 0 до V-1. В качестве значений истинности используются 1 и 0 (вместо True и False), чтобы сделать матрицу читабельной.

a, b, c, d, e, f, g, h = range(8)
# a b c d e f g h
N =  [[0,1,1,1,1,1,0,0], # a
  [0,0,1,0,1,0,0,0], # b
  [0,0,0,1,0,0,0,0], # c
  [0,0,0,0,1,0,0,0], # d
  [0,0,0,0,0,1,0,0], # e
  [0,0,1,0,0,0,1,1], # f
  [0,0,0,0,0,1,0,1], # g
  [0,0,0,0,0,1,1,0]] # h

Способ использования матриц смежности слегка отличается от списков и множеств смежности. Вместо проверки входит ли b в N[a], вы будете проверять, истинно ли значение ячейки матрицы N[a][b]. Кроме того, больше нельзя использовать len(N[a]), чтобы получить количество смежных вершин, потому что все ряды одной и той же длины. Вместо этого можно использовать функцию sum:

>>> N[a][b]
1
>>> sum(N[f])
3

Матрицы смежности имеют ряд полезных свойств, о которых стоит знать. Во-первых, так как мы не рассматриваем графы с петлями (т.е. не работаем с псевдографами), все значения на диагонали ложны. Также, ненаправленные графы обычно описываются парами ребер в обоих направлениях. Это значит, что матрица смежности для ненаправленного графа будет симметричной.


В теории графов очень часто встречается понятие разреженных матриц. Поэтому нужно задуматься, как их лучше всего представлять в Python. К счатью уже давно имеется стандартный подход к решению данной проблемы.

                            3      0     -2     11
                            0      9      0      0
                            0      7      0      0
                            0      0      0     -5
Существует  стандартный способ представлять матрицу посредством списка списков:

matrix = [[3, 0, -2, 11], [0, 9, 0, 0], [0, 7, 0, 0], [0, 0, 0, -5]]
К элементам  матрицы можно обращаться по номеру столбца и строки:

element = matrix [rownum] [colnum]

Однако в некоторых матрицах большиснство элементов нулевые. Чтобы не использовать память под всю матрицу, можно сохранять только ненулевые элементы. Такие представления называются разреженными матрицами. Например, разреженная матрица могла бы представляться следующим образом:
matrix = {(0, 0):3, (0, 2):-2, (0, 3):11, (1, 1):9, (2, 1):7, (3, 3):5}

Теперь к  элементу матрицы можно обращаться следующим образом:matrix.get((0,1), 0), второй аргумент - это возвращаемое значение
при отсутствии данного ключа (в нашем случае (0,1))

Расширение матрицы смежности для использования весов тривиально: вместо сохранения логических значений, сохраняйте значения весов. В случае с ребром (u, v) N[u][v] будет весом ребра w(u,v) вместо True. Часто в практических целях несуществующим ребрам присваиваются бесконечные веса. (Это гарантирует, что они не будут включены, например, в кратчайшие пути, т. к. мы ищем путь по существующим ребрам). Не всегда очевидно, как представить бесконечность, но совершенно точно есть несколько разных вариантов.

Один из них состоит в том, чтобы использовать некорректное для веса значение, такое как None или -1, если известно, что все веса неотрицательны. Возможно, в ряде случаев полезно использовать действительно большие числа. Для целых весов можно применить sys.maxint, хотя это значение и не обязательно самое большое (длинные целые могут быть больше). Есть и значение, введенное для отражения бесконечности: inf. Оно недоступно в Python напрямую по имени и выражается как float('inf')(гарантируется, что это работает для Python 2.6 и старше. В ранних версиях подобные специальные значения были платформо-зависимы, хотя float('inf') или float('Inf') должны сработать на большинстве платформ).

Листинг ниже показывает, как выглядит матрица весов, реализованная вложенными списками. Использованы те же веса, что и в листинге выше.

a, b, c, d, e, f, g, h = range(8)
_ = float('inf')
  # a b c d e f g h
W = [[0,2,1,3,9,4,_,_], # a
   [_,0,4,_,3,_,_,_], # b
  [_,_,0,8,_,_,_,_], # c
  [_,_,_,0,7,_,_,_], # d
  [_,_,_,_,0,5,_,_], # e
  [_,_,2,_,_,0,2,2], # f
  [_,_,_,_,_,1,0,6], # g
  [_,_,_,_,_,9,8,0]] # h

Бесконечное значение обозначено как подчеркивание (_), потому что это коротко и визуально различимо. Естественно, можно использовать любое имя, которое вы предпочтете. Обратите внимание, что значения на диагонали по-прежнему равны нулю, потому что даже без учета петель, веса часто интерпретируются как расстояния, а расстояние от вершины до самой себя равно нулю.

Конечно, матрицы весов дают возможность очень просто получить веса ребер, но, к примеру, проверка смежности и определение степени вершины, или обход всех смежных вершин делаются иначе. Здесь нужно использовать бесконечное значение, примерно так (для большей наглядности определим inf = float('inf')):

>>> W[a][b] < inf # смежность
True
>>> W[c][e] < inf # смежность
False
>>> sum(1 for w in W[a] if w < inf) - 1 # степень
5

Обратите внимание, что из полученной степени вычитается 1, потому что мы не считаем значения на диагонали. Сложность вычисления степени тут Θ(n), в то время как в другом представлении и смежность, и степень вершины можно определить за константное время. Так что вы всегда должны понимать, как именно вы собираетесь использовать ваш граф и выбирать для него соответствующее представление.

Представления графов. Структуры Вирта 
 

    Для представления графа в памяти ЭВМ существует подход Никлауса Вирта, который предполагает построение динамической структуры со многими связями. Вершины графа представляются линейным списком, состоящим из заголовочных узлов. Каждый заголовочный узел содержит четыре поля.

    Если указатель P указывает на заголовочный узел, представляющий вершину Q графа, то:

• поле (*P).Key содержит информацию, связанную с вершиной Q;
• поле (*P).Count содержит количество входящик дуг;
• поле (*P).Next содержит указатель на заголовочный узел, представляющий следующую вершину графа (если такая вершина есть) в списке заголовочных узлов;
• каждый заголовочный узел является заглавным звеном списка узлов второго типа, называемых дуговыми узлами. Такой список мы будем называть списком смежности. Поле (*P).Trail указывает на список смежности, представляющий дуги, выходящие из вершины Q графа (английское слово "Trail" переводится как "тащиться, свисать, волочиться").

    Каждый узел списка смежности содержит два поля: Id и Next, причем если Q указывает на дуговой узел, представляющий дугу (A,B), то:

• поле (*Q).Id указывает на заголовочный узел, представляющий вершину B графа;
• поле (*Q).Next указывает на дуговой узел, представляющий следующую дугу, выходящую из вершины A графа (если такая дуга есть).

    Каждый дуговой узел содержится в единственном списке смежности, представляющем все дуги, выходящие из данной вершины графа.

    Вывод. Каждый заголовочный узел содержит поля Key, Count и два указателя:

• первый указывает на список смежных дуг, выходящих из вершины графа,
• второй - на следующий заголовочный узел в списке заголовочных узлов.

    Каждый дуговой узел содержит два указателя:

• на следующий дуговой узел в списке смежности и
• на заголовочный узел, представляющий ту вершину графа, которая является концом дуги.

    На рисунке показан ориентированный граф и его представление с помощью структуры Вирта (символ N обозначает None):

Рис.1. Представление графа с помощью структуры Вирта

Рассмотрим пример создания данной структуры на Python.

class  Leader:
    def __init__(self, key, count, next, trail):
        self.Key=key
        self.Count=count
        self.Trail=trail
        self.Next=next


class Trailer:
    def __init__(self, id, next):
        self.Id=id
        self.Next=next

#Воссоздадим структуру с рисунка
q8=Leader(8,0,None,None)
t21=Trailer(q8,None)
q2=Leader(2,1,q8,t21)
t51=Trailer(q8,None)
q5=Leader(5,1,q2,t51)
t41=Trailer(q8,None)
q4=Leader(4,1,q5,t41)
t12=Trailer(q2,None)
t11=Trailer(q4,t12)
q1=Leader(1,2,q4,t11)

 Всем бы хорошо, только не удобно создавать структуру Вирта таким способом. Мне кажется, что куда удобнее подавать на вход граф в виде словаря, например для данного графа:
Edges = {'1':['2','4'], '2':['8'], '4':['8'], '5':['8'], '8':[]} и на выходе получить нужную нам структуру.
Поэтому я написал такую вот функцию:

#Создание структуры Вирта
def ceateVirtStructLeader(edges):
    q=[]
    stack=dict()
    
    #количество исходящих дуг
    def col(name):
        col=0
        for node in edges.keys():
            col+=edges[node].count(name)
        return col
    
    def ReverseLoop(elem, flag=0):
        elem.reverse()
        k=None
        for node in elem:
            node.Next=k
            if node.__class__.__name__=="Leader":node.Trail=ceateVirtStructTrailer(edges[node.Key])
            k=node
        return node
        
    #создание Trailer'ов
    def ceateVirtStructTrailer(ledges):
        if ledges!=[]:
            t=[]
            for node in ledges:
                trail=Trailer(stack[node], None)
                t.append(trail)
            return ReverseLoop(t)
        return None
    
    for node in edges.keys():
        lead=Leader(node,col(node),None,None)
        q.append(lead)
        stack[node]=lead
    return ReverseLoop(q)

Полезный пример работы с такой структурой описан в статье по топологической сортировке.
Так же существует модифицированная структура Вирта.

Массивы специального назначения из NumPy

Библиотека NumPy содержит много функциональности, связанной с 

многомерными массивами. Для представления графов большая ее часть 

не нужна, но массивы из NumPy весьма полезны, например, для реализации 

матриц весов или смежности.

Вместо создания пустой матрицы весов или смежности из списков для n вершин, 

вроде такого:
>>> N = [[0]*10 for i in range(10)]

в NumPy можно использовать функцию zeros:
>>> import numpy as np
>>> N = np.zeros([10,10])

Отдельные элементы доступны по индексам, разделенным запятой: A[u,v]. 

Чтобы получить соседние с данной вершины, используется одиночный индекс: A[u].
Пакет NumPy можно получить по адресу http://numpy.scipy.org.
Имейте ввиду, что вам нужна та версия NumPy, что будет работать с вашей версией 

Python. Если последний релиз NumPy не поддерживает ту версию Python, что вы 

используете, вы можете скомпилировать и установить библиотеку прямо из 

репозитория исходных кодов. Исходный код можно получить с помощью следующих 

команд (предполагается, что у вас установлена Subversion):
svn co http://svn.scipy.org/svn/numpy/trunk numpy
Больше информации о том, как компилировать и устанавливать NumPy, так же как и 

подробную документацию, можно найти на сайте библиотеки.

Реализация деревьев

Любое представление графов, естественно, можно использовать для представления деревьев, потому что деревья — это особый вид графов. Однако, деревья играют свою большую роль в алгоритмах, и для них разработано много соответствующих структур и методов. Большинство алгоритмов на деревьях (например, поиск по деревьям) можно рассматривать в терминах теории графов, но специальные структуры данных делают их проще в реализации.
Проще всего описать представление дерева с корнем, в котором ребра спускаются вниз от корня. Такие деревья часто отображают иерархическое ветвление данных, где корень отображает все объекты (которые, возможно, хранятся в листьях), а каждый внутренний узел показывает объекты, содержащиеся в дереве, корень которого — этот узел. Это описание можно использовать, представив каждое поддерево списком, содержащим все его поддеревья-потомки. Рассмотрим простое дерево, показанное на рисунке. 2.
Мы можем представить это дерево как список списков:

>>> T = [["a", "b"], ["c"], ["d", ["e", "f"]]]
>>> T[0][1]
'b'
>>> T[2][1][0]
'e'

Каждый список в сущности является списком потомков каждого из внутренних узлов. Во втором примере мы обращаемся к третьему потомку корня, затем ко второму его потомку и в конце концов — к первому потомку предыдущего узла (этот путь отмечен на рисунке).


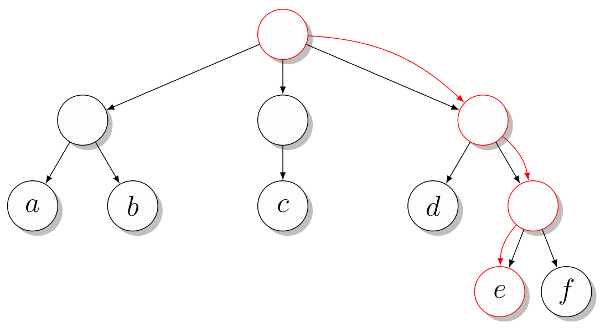
Рис. 2. Пример дерева с отмеченным путем от корня к листу

В ряде случаев возможно заранее определить максимальное число потомков каждого узла. (Например, каждый узел бинарного дерева может иметь до двух потомков). Поэтому можно использовать другие представления, скажем, объекты с отдельным атрибутом для каждого из потомков как в листинге ниже.

class Tree:
 def __init__(self, left, right):
  self.left = left
  self.right = right
>>> t = Tree(Tree("a", "b"), Tree("c", "d"))
>>> t.right.left
'c'

Для обозначения отсутствующих потомков можно использовать None (в случае если у узла только один потомок). Само собой, можно комбинировать разные методы (например, использовать списки или множества потомков для каждого узла).

Распространенный способ реализации деревьев, особенно на языках, не имеющих встроенной поддержки списков, это так называемое представление «первый потомок, следующий брат». В нем каждый узел имеет два «указателя» или атрибута, указывающих на другие узлы, как в бинарном дереве. Однако, первый из этих атрибутов ссылается на первого потомка узла, а второй — на его следующего брата (т.е. узел, имеющий того же родителя, но находящийся правее, — прим. перев). Иными словами, каждый узел дерева имеет указатель на связанный список его потомков, а каждый из этих потомков ссылается на свой собственный аналогичный список. Таким образом, небольшая модификация бинарного дерева даст нам многопутевое дерево, показанное в листинге ниже.

class Tree:
 def __init__(self, kids, next=None):
  self.kids = self.val = kids
  self.next = next

Отдельный атрибут val здесь введен просто для того, чтобы получить понятный вывод при указании значения (например, «c») вместо ссылки на узел. Естественно, все это можно изменять. Вот пример того, как можно обращаться с этой структурой:

>>> t = Tree(Tree("a", Tree("b", Tree("c", Tree("d")))))
>>> t.kids.next.next.val
'c'

А вот как выглядит это дерево:


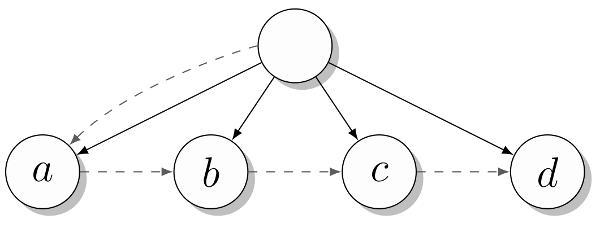
Атрибуты kids и next показаны пунктирными линиями, а сами ребра дерева — сплошными. Я немного схитрил и не стал показывать отдельные узлы для строк «a», «b» и т.д. Вместо этого я трактую их как метки на соответствующих родительских узлах. В более сложном дереве вместо использования одного атрибута и для хранения значения узла и для ссылки на список потомков, для обеих целей могут понадобиться отдельный атрибуты. Обычно для обхода дерева используется более сложный код (включая циклы и рекурсию), чем приведенный здесь с жестко заданным путем.

Шаблон проектирования «Набор»

При проектировании (да и реализации) таких структур данных как 

деревья может оказаться полезным гибкий класс, позволяющий задавать 

набор атрибутов через конструктор. Здесь нас может выручить шаблон 

проектирования «Набор» (названный так Алексом Мартелли в 

«Python Cookbook»). Есть много способов его реализации, но суть видна 

из следующего кода:
class Bunch(dict):
 def __init__(self, *args, **kwds):
  super(Bunch, self).__init__(*args, **kwds)
  self.__dict__ = self
Есть несколько полезных способов его применения. Во-первых, он позволяет 

создать и задать значения атрибутов, передав их как аргументы при создании 

объекта:
>>> x = Bunch(name="Jayne Cobb", position="PR")
>>> x.name
'Jayne Cobb'
Во-вторых, наследование от dict дает много дополнительного функционала, 

такого как получение всех ключей (атрибутов) или простая проверка наличия 

атрибута. 

Вот пример:
>>> T = Bunch
>>> t = T(left=T(left="a", right="b"), right=T(left="c"))
>>> t.left
{'right': 'b', 'left': 'a'}
>>> t.left.right
'b'
>>> t['left']['right']
'b'
>>> "left" in t.right
True
>>> "right" in t.right
False
Конечно же этот шаблон можно использовать не только для создания деревьев. 

Он пригодится в любой ситуации, где необходим гибкий объект, умеющий задавать 

свои атрибуты при создании.

Множество разных представлений

Несмотря на то, что существует масса представлений графов, большинство изучают и используют только два вида (с изменениями), уже описанных в этой главе. Джереми Спинред в своей книге «Effective Graph Representation» пишет, что его, как исследователя компьютерного представления графов, «особенно раздражают» большинство вводных статей. Приводимые в них описания хорошо известных представлений (списков и матриц смежности) обычно адекватны, но более общие объяснения нередко ошибочны. Как пример он показывает следующий ложный вывод о представлении графов, который основывается на неверных положениях из разных статей:
«Существует два метода представления графов в компьютере: списки и матрицы смежности. Работа с матрицами смежности быстрее, но они требуют больше памяти, чем списки смежности, так что вам нужно выбрать один из двух способов, исходя из того, какой ресурс для вас важнее» 
Пример реализации основанный на списках можно найти в статье Деревья кодирования по Хаффману

Спинред отмечает, что эти заключения сомнительны по нескольким причинам. Во-первых, есть много интересных способов представления графов, не только два описанных. Например, существуют списки ребер (или множества ребер), являющиеся списком всех ребер в виде пар вершин (или специальных объектов-ребер), существуют матрицы инцидентности, показывающие, какие ребра каким вершинам инцидентны (полезно для мультиграфов). Также существуют специальные методы для особых типов графов, вроде деревьев (описанных выше) и интервальных графов (здесь не рассматриваются). Полистайте книгу Спинреда, чтобы узнать о представлениях графов, которые вам могут когда-нибудь понадобиться.

Во-вторых, идея компромисса между памятью и временем работы может ввести в заблуждение: есть проблемы, решение которых со списками смежности будет быстрее, чем с матрицами смежности, а для произвольного графа на практике списки смежности требуют больше памяти, чем матрицы.

Так что, вместо того, чтобы полагаться на простые обобщенные выводы, подобные описаным, нужно вникнуть в специфику своей задачи. Основным критерием, вероятно, будет асимптотическая сложность того, что вы делаете. Например, поиск ребра (u, v) в матрице смежности выполняется за Θ(1), а обход смежных с v вершин — за Θ(n), в то время как на списке смежности обе операции будут выполнены за Θ(d(v)), т.е. будут зависеть от количества смежных с данной вершин.

Если асимптотическая сложность вашего алгоритма не зависит от типа представления, вы можете провести какие-либо эмпирические тесты, описанные ранее в этой главе. Или, как часто и бывает, можно выбрать то представление, которое лучше сочетается с вашим кодом и проще в поддержке.
Важный способ использования графов, который еще не был затронут, не касается их представления. Дело в том, что во многих задачах данные уже имеют структуру графа, или даже дерева, и мы можем использовать для них соответствующие алгоритмы для графов и деревьев без создания специальных представлений. В ряде случаев это происходит, если представление графа составлено вне нашей программы. Например, при разборе XML-документов или обходе каталогов файловой системы древовидная структура уже создана и для нее существуют определенные API. Иными словами, мы неявно задаем граф. К примеру, чтобы найти наиболее эффективное решение для заданной конфигурации кубика Рубика, можно определить состояние кубика и методы его изменения. Но даже если явно не описывать и не сохранять каждую конфигурацию, возможные состояния сформируют неявный граф (или множество вершин) с ребрами — операторами изменения состояния. Дальше можно использовать такие алгоритмы, как A* или двунаправленный алгоритм Дейкстры, чтобы найти кратчайший путь до состояния решения. В таких случаях функция получения соседних вершин N(v) будет работать «на лету», вероятно, возвращая смежные вершины как коллекцию или другую форму объекта-итератора.

И последний тип графов, которого я коснусь в этой главе, называется графом подзадач. Это глубокая концепция, к которой я еще неоднократно буду обращаться, описывая различные техники построения алгоритмов. Вкратце, большинство задач может быть разложено на подзадачи: меньшие задачи, часто имеющие похожую структуру. Они формируют вершины графа подзадач, а их зависимости (т.е. какая подзадача от какой зависит) выражаются ребрами. И хотя алгоритмы на графы редко применяются на графах подзадач (они используются больше как инструмент анализа), такие графы отлично позволяют понять технику «разделяй и властвуй» и динамическое программирование.


Используемая литература:

1. Словари
2. Реализация графов и деревьев на Python
3. Структура Вирта