Предлагаю чуточку отвлечься от Sython'a (я так называю реализацию SICP на Python))))
Итак рассмотрим один из простых но очень классических алгоритмов - алгоритм Прима поиска минимальных остовного дерева.
Советую так же ознакомиться со статьей Теория графов и деревьев для Python
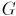 с
с 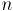 вершинами и
вершинами и 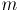 рёбрами. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим возможным весом (т.е. суммой весов рёбер). Поддерево — это набор рёбер, соединяющих все вершины, причём из любой вершины можно добраться до любой другой ровно одним простым путём.
рёбрами. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим возможным весом (т.е. суммой весов рёбер). Поддерево — это набор рёбер, соединяющих все вершины, причём из любой вершины можно добраться до любой другой ровно одним простым путём.
*-Нравится статья? Кликни по рекламе! :)
Сам алгоритм имеет очень простой вид. Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой — наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого — уже взятая в остов вершина, а другой конец — ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины (или, что то же самое,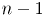 ребро).
ребро).
В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет (количество выбранных рёбер останется меньше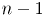 ).
).
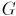 был связным, т.е. ответ существует. Обозначим через
был связным, т.е. ответ существует. Обозначим через 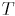 остов, найденный алгоритмом Прима, а через
остов, найденный алгоритмом Прима, а через 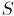 — минимальный остов. Очевидно, что
— минимальный остов. Очевидно, что 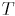 действительно является остовом (т.е. поддеревом графа
действительно является остовом (т.е. поддеревом графа 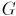 ). Покажем, что веса
). Покажем, что веса 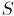 и
и 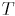 совпадают.
совпадают.
Рассмотрим первый момент времени, когда в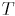 происходило добавление ребра, не входящего в оптимальный остов
происходило добавление ребра, не входящего в оптимальный остов 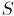 . Обозначим это ребро через
. Обозначим это ребро через 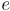 , концы его — через
, концы его — через 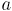 и
и 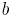 , а множество входящих на тот момент в остов вершин — через
, а множество входящих на тот момент в остов вершин — через 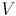 (согласно алгоритму,
(согласно алгоритму, 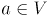 ,
, 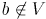 , либо наоборот). В оптимальном остове
, либо наоборот). В оптимальном остове 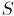 вершины
вершины 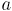 и
и 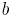 соединяются каким-то путём
соединяются каким-то путём 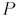 ; найдём в этом пути любое ребро
; найдём в этом пути любое ребро 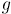 , один конец которого лежит в
, один конец которого лежит в 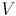 , а другой — нет. Поскольку алгоритм Прима выбрал ребро
, а другой — нет. Поскольку алгоритм Прима выбрал ребро 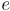 вместо ребра
вместо ребра 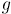 , то это значит, что вес ребра
, то это значит, что вес ребра 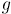 больше либо равен весу ребра
больше либо равен весу ребра 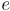 .
.
Удалим теперь из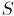 ребро
ребро 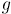 , и добавим ребро
, и добавим ребро 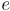 . По только что сказанному, вес остова в результате не мог увеличиться (уменьшиться он тоже не мог, поскольку
. По только что сказанному, вес остова в результате не мог увеличиться (уменьшиться он тоже не мог, поскольку 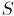 было оптимальным). Кроме того,
было оптимальным). Кроме того, 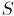 не перестало быть остовом (в том, что связность не нарушилась, нетрудно убедиться: мы замкнули путь
не перестало быть остовом (в том, что связность не нарушилась, нетрудно убедиться: мы замкнули путь 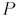 в цикл, и потом удалили из этого цикла одно ребро).
в цикл, и потом удалили из этого цикла одно ребро).
Итак, мы показали, что можно выбрать оптимальный остов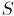 таким образом, что он будет включать ребро
таким образом, что он будет включать ребро 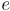 . Повторяя эту процедуру необходимое число раз, мы получаем, что можно выбрать оптимальный остов
. Повторяя эту процедуру необходимое число раз, мы получаем, что можно выбрать оптимальный остов 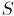 так, чтобы он совпадал с
так, чтобы он совпадал с 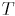 . Следовательно, вес построенного алгоритмом Прима
. Следовательно, вес построенного алгоритмом Прима 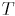 минимален, что и требовалось доказать.
минимален, что и требовалось доказать.
Тривиальная реализация: алгоритмы за
Если искать каждый раз ребро простым просмотром среди всех возможных вариантов, то асимптотически будет требоваться просмотр 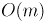 рёбер, чтобы найти среди всех допустимых ребро с наименьшим весом. Суммарная асимптотика алгоритма составит в таком случае
рёбер, чтобы найти среди всех допустимых ребро с наименьшим весом. Суммарная асимптотика алгоритма составит в таком случае 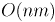 , что в худшем случае есть
, что в худшем случае есть 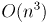 , — слишком медленный алгоритм.
, — слишком медленный алгоритм.
Этот алгоритм можно улучшить, если просматривать каждый раз не все рёбра, а только по одному ребру из каждой уже выбранной вершины. Для этого, например, можно отсортировать рёбра из каждой вершины в порядке возрастания весов, и хранить указатель на первое допустимое ребро (напомним, допустимы только те рёбра, которые ведут в множество ещё не выбранных вершин). Тогда, если пересчитывать эти указатели при каждом добавлении ребра в остов, суммарная асимптотика алгоритма будет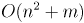 , но предварительно потребуется выполнить сортировку всех рёбер за
, но предварительно потребуется выполнить сортировку всех рёбер за 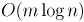 , что в худшем случае (для плотных графов) даёт асимптотику
, что в худшем случае (для плотных графов) даёт асимптотику 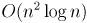 .
.
Ниже мы рассмотрим два немного других алгоритма: для плотных и для разреженных графов, получив в итоге заметно лучшую асимптотику.
Случай плотных графов: алгоритм за
Подойдём к вопросу поиска наименьшего ребра с другой стороны: для каждой ещё не выбранной будем хранить минимальное ребро, ведущее в уже выбранную вершину.
Тогда, чтобы на текущем шаге произвести выбор минимального ребра, надо просто просмотреть эти минимальные рёбра у каждой не выбранной ещё вершины — асимптотика составит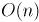 .
.
Но теперь при добавлении в остов очередного ребра и вершины эти указатели надо пересчитывать. Заметим, что эти указатели могут только уменьшаться, т.е. у каждой не просмотренной ещё вершины надо либо оставить её указатель без изменения, либо присвоить ему вес ребра в только что добавленную вершину. Следовательно, эту фазу можно сделать также за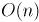 .
.
Таким образом, мы получили вариант алгоритма Прима с асимптотикой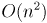 .
.
В частности, такая реализация особенно удобна для решения так называемой евклидовой задачи о минимальном остове: когда даны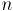 точек на плоскости, расстояние между которыми измеряется по стандартной евклидовой метрике, и требуется найти остов минимального веса, соединяющий их все (причём добавлять новые вершины где-либо в других местах запрещается). Эта задача решается описанным здесь алгоритмом за
точек на плоскости, расстояние между которыми измеряется по стандартной евклидовой метрике, и требуется найти остов минимального веса, соединяющий их все (причём добавлять новые вершины где-либо в других местах запрещается). Эта задача решается описанным здесь алгоритмом за 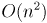 времени и
времени и 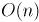 памяти, чего не получится добиться алгоритмом Крускала.
памяти, чего не получится добиться алгоритмом Крускала.
Случай разреженных графов: алгоритм за
В описанном выше алгоритме можно увидеть стандартные операции нахождения минимума в множестве и изменение значений в этом множестве. Эти две операции являются классическими, и выполняются многими структурами данных, например, реализованным в языке C++ красно-чёрным деревом set.
По смыслу алгоритм остаётся точно таким же, однако теперь мы можем найти минимальное ребро за время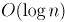 . С другой стороны, время на пересчёт
. С другой стороны, время на пересчёт 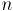 указателей теперь составит
указателей теперь составит 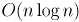 , что хуже, чем в вышеописанном алгоритме.
, что хуже, чем в вышеописанном алгоритме.
Если учесть, что всего будет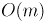 пересчётов указателей и
пересчётов указателей и 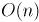 поисков минимального ребра, то суммарная асимптотика составит
поисков минимального ребра, то суммарная асимптотика составит 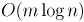 — для разреженных графов это лучше, чем оба вышеописанных алгоритма, но на плотных графах этот алгоритм будет медленнее предыдущего.
— для разреженных графов это лучше, чем оба вышеописанных алгоритма, но на плотных графах этот алгоритм будет медленнее предыдущего.
Реализация на Python(за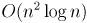 )
)
На сайте Традиция представлен данный алгоритм на Python, но мне кажется, что это выдранный кусочек кода, т.к. совсем не понятно какого класса объект G подается на вход функции, поэтому относитесь к нему как к псевдокоду))) Но там так же представлена иллюстрация к алгоритму, наш пример мы построим именно на том графе.
Для представления воспользуемся так называемой смежной весовой матрицей. Которая симметрична относительно своей главной, нулевой(т.е. она заполнена 0) диагонали. Примем, что -1 означает отсутствие маршрута между городами, как между Минском и NY))
mnsk NY mos ber kiv
mnsk 0 -1 15 20 15
NY -1 0 60 50 80
mos 15 60 0 50 10
ber 20 50 50 0 30
kiv 15 80 10 30 0
Воспользуемся стандартным способом представлять матрицу посредством списка списков:
Вот наши функции:
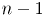 фаза, на каждой из которых сначала выбирается оптимальное ребро, добавляется в ответ, а затем пересчитываются значения для всех не выбранных ещё вершин). Более того, алгоритм Дейкстры тоже имеет два варианта реализации: за
фаза, на каждой из которых сначала выбирается оптимальное ребро, добавляется в ответ, а затем пересчитываются значения для всех не выбранных ещё вершин). Более того, алгоритм Дейкстры тоже имеет два варианта реализации: за 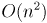 и
и 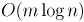 (мы, конечно, здесь не учитываем возможность использования сложных структур данных для достижения ещё меньших асимптотик).
(мы, конечно, здесь не учитываем возможность использования сложных структур данных для достижения ещё меньших асимптотик).
Если взглянуть на алгоритмы Прима и Дейкстры более формально, то получается, что они вообще идентичны друг другу, за исключением весовой функции вершин: если в алгоритме Дейкстры у каждой вершины поддерживается длина кратчайшего пути (т.е. сумма весов некоторых рёбер), то в алгоритме Прима каждой вершине приписывается только вес минимального ребра, ведущего в множество уже взятых вершин.
Итак рассмотрим один из простых но очень классических алгоритмов - алгоритм Прима поиска минимальных остовного дерева.
Советую так же ознакомиться со статьей Теория графов и деревьев для Python
Описание
Дан взвешенный неориентированный граф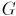 с
с 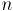 вершинами и
вершинами и 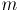 рёбрами. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим возможным весом (т.е. суммой весов рёбер). Поддерево — это набор рёбер, соединяющих все вершины, причём из любой вершины можно добраться до любой другой ровно одним простым путём.
рёбрами. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим возможным весом (т.е. суммой весов рёбер). Поддерево — это набор рёбер, соединяющих все вершины, причём из любой вершины можно добраться до любой другой ровно одним простым путём.*-Нравится статья? Кликни по рекламе! :)
Сам алгоритм имеет очень простой вид. Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой — наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого — уже взятая в остов вершина, а другой конец — ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины (или, что то же самое,
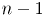 ребро).
ребро).В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет (количество выбранных рёбер останется меньше
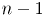 ).
).Доказательство
Пусть граф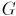 был связным, т.е. ответ существует. Обозначим через
был связным, т.е. ответ существует. Обозначим через 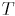 остов, найденный алгоритмом Прима, а через
остов, найденный алгоритмом Прима, а через 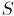 — минимальный остов. Очевидно, что
— минимальный остов. Очевидно, что 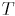 действительно является остовом (т.е. поддеревом графа
действительно является остовом (т.е. поддеревом графа 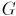 ). Покажем, что веса
). Покажем, что веса 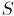 и
и 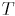 совпадают.
совпадают.Рассмотрим первый момент времени, когда в
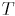 происходило добавление ребра, не входящего в оптимальный остов
происходило добавление ребра, не входящего в оптимальный остов 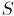 . Обозначим это ребро через
. Обозначим это ребро через 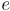 , концы его — через
, концы его — через 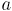 и
и 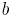 , а множество входящих на тот момент в остов вершин — через
, а множество входящих на тот момент в остов вершин — через 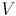 (согласно алгоритму,
(согласно алгоритму, 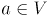 ,
, 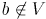 , либо наоборот). В оптимальном остове
, либо наоборот). В оптимальном остове 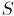 вершины
вершины 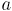 и
и 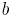 соединяются каким-то путём
соединяются каким-то путём 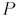 ; найдём в этом пути любое ребро
; найдём в этом пути любое ребро 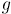 , один конец которого лежит в
, один конец которого лежит в 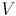 , а другой — нет. Поскольку алгоритм Прима выбрал ребро
, а другой — нет. Поскольку алгоритм Прима выбрал ребро 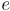 вместо ребра
вместо ребра 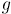 , то это значит, что вес ребра
, то это значит, что вес ребра 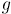 больше либо равен весу ребра
больше либо равен весу ребра 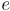 .
.Удалим теперь из
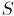 ребро
ребро 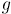 , и добавим ребро
, и добавим ребро 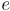 . По только что сказанному, вес остова в результате не мог увеличиться (уменьшиться он тоже не мог, поскольку
. По только что сказанному, вес остова в результате не мог увеличиться (уменьшиться он тоже не мог, поскольку 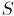 было оптимальным). Кроме того,
было оптимальным). Кроме того, 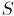 не перестало быть остовом (в том, что связность не нарушилась, нетрудно убедиться: мы замкнули путь
не перестало быть остовом (в том, что связность не нарушилась, нетрудно убедиться: мы замкнули путь 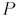 в цикл, и потом удалили из этого цикла одно ребро).
в цикл, и потом удалили из этого цикла одно ребро).Итак, мы показали, что можно выбрать оптимальный остов
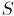 таким образом, что он будет включать ребро
таким образом, что он будет включать ребро 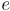 . Повторяя эту процедуру необходимое число раз, мы получаем, что можно выбрать оптимальный остов
. Повторяя эту процедуру необходимое число раз, мы получаем, что можно выбрать оптимальный остов 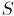 так, чтобы он совпадал с
так, чтобы он совпадал с 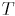 . Следовательно, вес построенного алгоритмом Прима
. Следовательно, вес построенного алгоритмом Прима 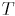 минимален, что и требовалось доказать.
минимален, что и требовалось доказать.Реализации
Время работы алгоритма существенно зависит от того, каким образом мы производим поиск очередного минимального ребра среди подходящих рёбер. Здесь могут быть разные подходы, приводящие к разным асимптотикам и разным реализациям.
Тривиальная реализация: алгоритмы за 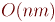 и
и 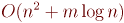
Если искать каждый раз ребро простым просмотром среди всех возможных вариантов, то асимптотически будет требоваться просмотр 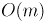 рёбер, чтобы найти среди всех допустимых ребро с наименьшим весом. Суммарная асимптотика алгоритма составит в таком случае
рёбер, чтобы найти среди всех допустимых ребро с наименьшим весом. Суммарная асимптотика алгоритма составит в таком случае 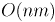 , что в худшем случае есть
, что в худшем случае есть 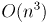 , — слишком медленный алгоритм.
, — слишком медленный алгоритм.Этот алгоритм можно улучшить, если просматривать каждый раз не все рёбра, а только по одному ребру из каждой уже выбранной вершины. Для этого, например, можно отсортировать рёбра из каждой вершины в порядке возрастания весов, и хранить указатель на первое допустимое ребро (напомним, допустимы только те рёбра, которые ведут в множество ещё не выбранных вершин). Тогда, если пересчитывать эти указатели при каждом добавлении ребра в остов, суммарная асимптотика алгоритма будет
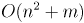 , но предварительно потребуется выполнить сортировку всех рёбер за
, но предварительно потребуется выполнить сортировку всех рёбер за 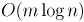 , что в худшем случае (для плотных графов) даёт асимптотику
, что в худшем случае (для плотных графов) даёт асимптотику 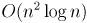 .
.Ниже мы рассмотрим два немного других алгоритма: для плотных и для разреженных графов, получив в итоге заметно лучшую асимптотику.
Случай плотных графов: алгоритм за 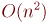
Подойдём к вопросу поиска наименьшего ребра с другой стороны: для каждой ещё не выбранной будем хранить минимальное ребро, ведущее в уже выбранную вершину.Тогда, чтобы на текущем шаге произвести выбор минимального ребра, надо просто просмотреть эти минимальные рёбра у каждой не выбранной ещё вершины — асимптотика составит
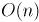 .
.Но теперь при добавлении в остов очередного ребра и вершины эти указатели надо пересчитывать. Заметим, что эти указатели могут только уменьшаться, т.е. у каждой не просмотренной ещё вершины надо либо оставить её указатель без изменения, либо присвоить ему вес ребра в только что добавленную вершину. Следовательно, эту фазу можно сделать также за
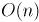 .
.Таким образом, мы получили вариант алгоритма Прима с асимптотикой
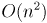 .
.В частности, такая реализация особенно удобна для решения так называемой евклидовой задачи о минимальном остове: когда даны
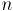 точек на плоскости, расстояние между которыми измеряется по стандартной евклидовой метрике, и требуется найти остов минимального веса, соединяющий их все (причём добавлять новые вершины где-либо в других местах запрещается). Эта задача решается описанным здесь алгоритмом за
точек на плоскости, расстояние между которыми измеряется по стандартной евклидовой метрике, и требуется найти остов минимального веса, соединяющий их все (причём добавлять новые вершины где-либо в других местах запрещается). Эта задача решается описанным здесь алгоритмом за 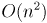 времени и
времени и 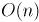 памяти, чего не получится добиться алгоритмом Крускала.
памяти, чего не получится добиться алгоритмом Крускала.
Случай разреженных графов: алгоритм за 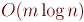
В описанном выше алгоритме можно увидеть стандартные операции нахождения минимума в множестве и изменение значений в этом множестве. Эти две операции являются классическими, и выполняются многими структурами данных, например, реализованным в языке C++ красно-чёрным деревом set.По смыслу алгоритм остаётся точно таким же, однако теперь мы можем найти минимальное ребро за время
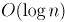 . С другой стороны, время на пересчёт
. С другой стороны, время на пересчёт 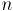 указателей теперь составит
указателей теперь составит 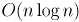 , что хуже, чем в вышеописанном алгоритме.
, что хуже, чем в вышеописанном алгоритме.Если учесть, что всего будет
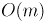 пересчётов указателей и
пересчётов указателей и 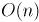 поисков минимального ребра, то суммарная асимптотика составит
поисков минимального ребра, то суммарная асимптотика составит 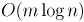 — для разреженных графов это лучше, чем оба вышеописанных алгоритма, но на плотных графах этот алгоритм будет медленнее предыдущего.
— для разреженных графов это лучше, чем оба вышеописанных алгоритма, но на плотных графах этот алгоритм будет медленнее предыдущего.Реализация на Python(за
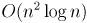 )
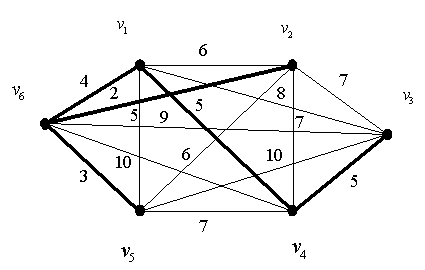
) На сайте Традиция представлен данный алгоритм на Python, но мне кажется, что это выдранный кусочек кода, т.к. совсем не понятно какого класса объект G подается на вход функции, поэтому относитесь к нему как к псевдокоду))) Но там так же представлена иллюстрация к алгоритму, наш пример мы построим именно на том графе.
Для представления воспользуемся так называемой смежной весовой матрицей. Которая симметрична относительно своей главной, нулевой(т.е. она заполнена 0) диагонали. Примем, что -1 означает отсутствие маршрута между городами, как между Минском и NY))
mnsk NY mos ber kiv
mnsk 0 -1 15 20 15
NY -1 0 60 50 80
mos 15 60 0 50 10
ber 20 50 50 0 30
kiv 15 80 10 30 0
Воспользуемся стандартным способом представлять матрицу посредством списка списков:
matr = [
[0, -1, 15, 20, 15],
[-1, 0, 60, 50, 80],
[15, 60, 0, 50, 10],
[20, 50, 50, 0, 30],
[15, 80, 10, 30, 0]
]
Вот наши функции:
def search_min(tr, vizited):#1 место для оптимизации
min=max(tr)
for ind in vizited:
for index, elem in enumerate(tr[ind]):
if elem>0 and elem<min and index not in vizited:
min=elem#веса путей
index2=index# индекс города
return [min, index2]
def prim(matr):
toVisit=[i for i in range(1,len(matr))]# города кроме начального(0)
vizited=[0]
result=[0]# начнем с минска
for index in toVisit:
weight, ind=search_min(matr, vizited)
result.append(weight)#в результат будут заноситься веса
vizited.append(ind)# содержит карту пути
return result
Аналогия с алгоритмом Дейкстры
Прослеживается вполне чёткая аналогия с алгоритмом Дейкстры: он имеет такую же структуру (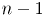 фаза, на каждой из которых сначала выбирается оптимальное ребро, добавляется в ответ, а затем пересчитываются значения для всех не выбранных ещё вершин). Более того, алгоритм Дейкстры тоже имеет два варианта реализации: за
фаза, на каждой из которых сначала выбирается оптимальное ребро, добавляется в ответ, а затем пересчитываются значения для всех не выбранных ещё вершин). Более того, алгоритм Дейкстры тоже имеет два варианта реализации: за 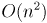 и
и 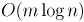 (мы, конечно, здесь не учитываем возможность использования сложных структур данных для достижения ещё меньших асимптотик).
(мы, конечно, здесь не учитываем возможность использования сложных структур данных для достижения ещё меньших асимптотик).Если взглянуть на алгоритмы Прима и Дейкстры более формально, то получается, что они вообще идентичны друг другу, за исключением весовой функции вершин: если в алгоритме Дейкстры у каждой вершины поддерживается длина кратчайшего пути (т.е. сумма весов некоторых рёбер), то в алгоритме Прима каждой вершине приписывается только вес минимального ребра, ведущего в множество уже взятых вершин.
Свойства минимальных остовов
- Максимальный остов также можно искать алгоритмом Прима (например, заменив все веса рёбер на противоположные: алгоритм не требует неотрицательности весов рёбер).
- Минимальный остов единственен, если веса всех рёбер различны. В противном случае, может существовать несколько минимальных остовов (какой именно будет выбран алгоритмом Прима, зависит от порядка просмотра рёбер/вершин с одинаковыми весами/указателями)
- Минимальный остов также является остовом, минимальным по произведению всех рёбер (предполагается, что все веса положительны). В самом деле, если мы заменим веса всех рёбер на их логарифмы, то легко заметить, что в работе алгоритма ничего не изменится, и будут найдены те же самые рёбра.
- Минимальный остов является остовом с минимальным весом самого тяжёлого ребра. Яснее всего это утверждение понятно, если рассмотреть работу алгоритма Крускала.
- Критерий минимальности остова: остов является минимальным тогда и только тогда, когда для любого ребра, не принадлежащего остову, цикл, образуемый этим ребром при добавлении к остову, не содержит рёбер тяжелее этого ребра. В самом деле, если для какого-то ребра оказалось, что оно легче некоторых рёбер образуемого цикла, то можно получить остов с меньшим весом (добавив это ребро в остов, и удалив самое тяжелое ребро из цикла). Если же это условие не выполнилось ни для одного ребра, то все эти рёбра не улучшают вес остова при их добавлении.

Отличный пост!
ОтветитьУдалитьСпасибо большое, очень полезно
ОтветитьУдалитьм
ОтветитьУдалитьХуй
ОтветитьУдалитьНе обзывайся, я поддерживаю данный сайт, ибо он хороший и помогает людям работать с графами
УдалитьКапец что тут у вас творится
ОтветитьУдалитьP.s. Код говно
ГОВНО ФУУУУУ ХУЙ ПОЗОР
ОтветитьУдалить