Что такое анализ?
Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Одну и ту же задачу можно решить с помощью различных алгоритмов. Анализ алгоритмов дает нам инструмент для выбора алгоритма.Результат анализа алгоритмов — не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Из статьи Порядок роста мы уже знаем, что разница между алгоритмом, который делает N + 5 операций, и тем, который делает N + 250 операций, становится незаметной, как только N становится очень большим.
*-Нравится статья? Кликни по рекламе! :)
Что подсчитывать и что учитывать?
- Аддитивные операции: сложение и вычитание.
- Мультипликативные операции: умножение, деление и взятие остатка по модулю.
- Особые: целочисленное умножение или деление на степень двойки сводятся к сдвигу, а он по скорости эквивалентен сложению.
Классы входных данных
При анализе алгоритма выбор входных данных может существенно повлиять на его выполнение. Скажем, некоторые алгоритмы сортировки могут работать очень быстро, если входной список уже отсортирован, тогда как другие алгоритмы покажут весьма скромный результат на таком списке. А вот на случайном списке результат может оказаться противоположным. Поэтому не будем ограничиваться анализом поведения алгоритмов на одном входном наборе данных. Практически нужно искать такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма. Кроме того, полезно оценивать и среднюю эффективность алгоритма на всех возможных наборах данных.
- Наилучший случай
- Наихудший случай
- Средний случай
Время выполнения алгоритма в наилучшем случае очень часто оказывается маленьким или просто постоянным, поэтому подобный анализ проводится редко.
Анализ наихудшего случая чрезвычайно важен, поскольку он позволяет представить максимальное время работы алгоритма. При анализе наихудшего случая необходимо найти входные данные, на которых алгоритм будет выполнять больше всего работы.
Анализ среднего случая является самым сложным, поскольку он требует учета множества разнообразных деталей. В основе анализа лежит определение различных групп, на которые следует разбить возможные входные наборы данных. На втором шаге определяется вероятность, с которой входной набор данных принадлежит каждой группе. На третьем шаге подсчитывается время работы алгоритма на данных из каждой группы. Время работы алгоритма на всех входных данных одной группы должно быть одинаковым, в противном случае группу следует подразбить. Среднее время работы вычисляется по формуле
где через n обозначен размер входных данных, через m — число групп. через pi — вероятность того, что входные данные принадлежат группе с номером i, а через ti — время, необходимое алгоритму для обработки данных из группы с номером i.
попасть в каждую группу равна 0.2. В этом случае среднее время работы можно либо оценить по предыдущей формуле, либо воспользоваться эквивалентной ей формулой
Нижние границы. Дерево решений.
Алгоритм является оптимальным, если любой любой другой алгоритм, решающий данную задачу, работает не быстрее данного. Как узнать оптимальность алгоритма? Для этого мы должны знать минимальное количество операций, необходимое для решения поставленной задачи, которое называется нижней границей. Но для этого нам нужно изучать именно ЗАДАЧУ, а не конкретный алгоритм!
Как пример, рассмотрим анализ процесса сортировки списка из 3 чисел, воспользовавшись бинарным деревом. Такое дерево называется деревом решений.
Самый длинный путь в данном дереве соответствует наихудшему случаю и наоборот, кратчайший - наилучшему. Средний случай описывается частным от деления числа ребер в дереве на число листов.
Для перестановки 2-х элементов мы имеем 1лист, для N эл-тов, по правилам комбинаторики, N! листов. Число листов на уровне K равно 2k-1, поэтому в нашем дереве решений буде L -уровней, где L - наименьшее целое число, для которого N! ≤ 2L-1. Логарифмируя, получим
В конечном итоге, получаем:
Вот мы и узнали, что любой алгоритм сортировки, порядка О(NlgN) является наилучшим и его можно считать оптимальным. Более того, из этого исследования вытекает, что алгоритм, решающий задачу сортировки быстрее О(NlgN) операций, не может работать правильно!
Используемая литература:
- Дж. Макконнелл - Основы современных алгоритмов.




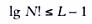



Комментариев нет:
Отправить комментарий