Связные списки

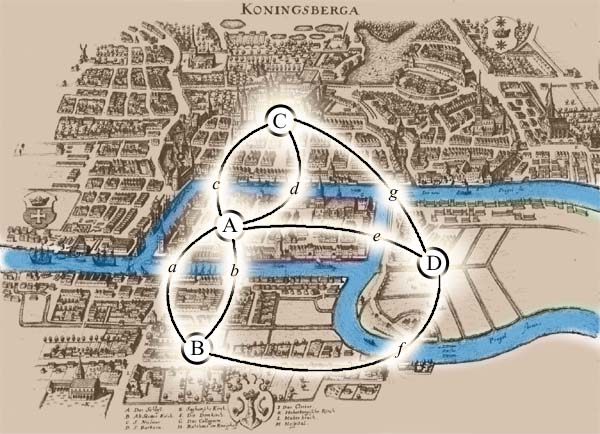
В информатике, свя́зный спи́сок — структура данных, состоящая из узлов, каждый из которых содержит как собственные данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка. Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.

Мы с вами рассмотрим реализацию односвязного (однонаправленного) списка.
*-Нравится статья? Кликни по рекламе! :)

Бинарные деревья

Бинарное дерево представляет собой структуру, в которой каждый узел (или вершина) имеет не более двух узлов-потомков и в точности одного родителя. Самый верхний узел дерева является единственным узлом без родителей; он называется корневым узлом. Бинарное дерево
с N узлами имеет не меньше [log₂N + 1] уровней (при максимально плотной упаковке узлов).
Если уровни дерева занумеровать, считая что корень лежит на уровне 1, то на уровне с номером К лежит 2^К-1 узел. У полного бинарного дерева с j уровнями (занумерованными от 1 до j) все листья лежат на уровне с номером j, и у каждого узла на уровнях с первого по j — 1
в точности два непосредственных потомка. В полном бинарном дереве с j уровнями 2^j — 1 узел.
*-Нравится статья? Кликни по рекламе! :)

Анализ алгоритма

Что такое анализ?

Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Одну и ту же задачу можно решить с помощью различных алгоритмов. Анализ алгоритмов дает нам инструмент для выбора алгоритма.
Результат анализа алгоритмов — не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Из статьи Порядок роста мы уже знаем, что разница между алгоритмом, который делает N + 5 операций, и тем, который делает N + 250 операций, становится незаметной, как только N становится очень большим.
*-Нравится статья? Кликни по рекламе! :)

Алгоритм Прима

Предлагаю чуточку отвлечься от Sython'a (я так называю реализацию SICP на Python))))
Итак рассмотрим один из простых но очень классических алгоритмов - алгоритм Прима поиска минимальных остовного дерева.
Советую так же ознакомиться со статьей Теория графов и деревьев для Python

Описание

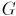Дан взвешенный неориентированный граф с 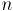вершинами и 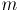рёбрами. Требуется найти такое поддерево этого графа, которое бы соединяло все его вершины, и при этом обладало наименьшим возможным весом (т.е. суммой весов рёбер). Поддерево — это набор рёбер, соединяющих все вершины, причём из любой вершины можно добраться до любой другой ровно одним простым путём.
*-Нравится статья? Кликни по рекламе! :)

Теория графов и деревьев для Python

 Многие задачи, например, задача обхода точек по кратчайшему маршруту, могут быть решены с помощью одного из мощнейших инструментов — с помощью графов. Часто, если вы можете определить, что решаете задачу на графы, вы по-крайней мере на полпути к решению. А если ваши данные можно каким-либо образом представить как деревья, у вас есть все шансы построить действительно эффективное решение.
Графами можно представить любую структуру или систему, от транспортной сети до сети передачи данных и от взаимодействия белков в ядре клетки до связей между людьми в Интернете.
*-Нравится статья? Кликни по рекламе! :)

Деревья кодирования по Хаффману

Эта статья дает возможность попрактиковаться в использовании списковых структур и абстракции данных для работы с множествами и деревьями.
Советую ознакомиться с предыдущей записью: Представление множеств и КодХаффмана
Они применяются к методам представления данных как последовательностей из единиц и нулей (битов). Например, стандартный код ASCII, который используется для представления текста в компьютерах, кодирует каждый символ как последовательность из семи бит. Семь бит позволяют нам обозначить 2⁷, то есть 128 различных символов. В общем случае, если нам требуется различать n символов, нам потребуется log₂N бит для каждого символа.
*-Нравится статья? Кликни по рекламе! :)

Представление множеств

И хотя в нашем любимом Python'е уже есть такой тип данных, как множества(set), я все таки считаю, Что изобрести велосипед заново, в данном случае будет полезно. Хотя бы чтобы просто получше понять, а как оно там вообще работает?!
Для понимания идеологии советую прочитать "Свойство замыкания на примере list"
*-Нравится статья? Кликни по рекламе! :)