Сортировка слиянием (англ. merge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи. Алгоритм был изобретён Джоном фон Нейманом в 1945 году.
Пример работы на последовательностях 2 3 6 7 и 1 4 5
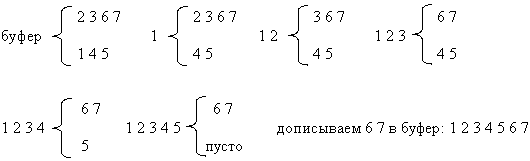 Результатом является упорядоченная последовательность, находящаяся в буфере. Каждая операция слияния требует n пересылок и n сравнений, где n - общее число элементов, так что время слияния: Theta(n).
Результатом является упорядоченная последовательность, находящаяся в буфере. Каждая операция слияния требует n пересылок и n сравнений, где n - общее число элементов, так что время слияния: Theta(n).
Ну что же, хватит слов, давайте реализовывать!)
Это был классический вариант с сайта алголист. Теперь я приведу пример 2-го алгоритма без дополнительного буфера и рекурсии. Но к сожалению всё вкусно не бывает, поэтому за всё нужно платить. Об этом смотри в результатах. А пока идея:
Она достаточно проста, но не так тривиальна, как в предыдущем алгоритме. Избавившись от рекурсии, мы обязаны следить за следованием промежуточных разбиений самостоятельно. Алгоритм начинает с того, что сравнивает каждые 2 соседних, объединяя их в 1 упорядоченный подмассив. Потом снова 2 соседних(но в каждом из них уже по 2 эл-та), потом так же, но по 4, 8, 16 и т.д. И чтобы не использовать буфер, мы итерационно переставляем элемента прям в памяти, , чтобы упорядочить их(это требует огромного числа перестановок((()
Еще 1 пример не рекурсивного алгоритма приведён на сайте википедии. Но там всё же вводится дополнительный буфер, равный размеру! массива.
Тестирование проводилось на списке из 5000 не повторяющихся элементов(как и в быстрой сортировке Хоара, чтобы можно было сравнить).
Хорошо запрограммированная внутренняя сортировка слиянием работает немного быстрее пирамидальной, но медленнее быстрой, при этом требуя много памяти под буфер. Поэтому mergeSort используют для упорядочения массивов, лишь если требуется устойчивость метода(которой нет ни у быстрой, ни у пирамидальной сортировок).
Странно, но мне показалось, что данный алгоритм не так сильно освещён в интернете в целом и на python в частности. А ведь именно этот алгоритм чаще всего применяется для сортировки данных не помещающихся в оперативке, т.е. хранящихся в файлах(внешние сортировки). Как и в случае с быстрой сортировкой Хоара, существует 2 реализации данного алгоритма. Рекурсивная и нет) Скажу по секрету, не рекурсивную реализацию мне предоставил так же мой преподаватель Деон. Более того, она ещё и не требует дополнительной памяти, что в классическом варианте относят к её основным минусам!
Для решения задачи сортировки эти три этапа выглядят так:
- Сортируемый массив разбивается на две части примерно одинакового размера;
- Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом;
- Два упорядоченных массива половинного размера соединяются в один.
Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным).
Нетривиальным этапом является соединение двух упорядоченных массивов в один. Основную идею слияния двух отсортированных массивов можно объяснить на следующем примере. Пусть мы имеем две стопки карт, лежащих рубашками вниз так, что в любой момент мы видим верхнюю карту в каждой из этих стопок. Пусть также, карты в каждой из этих стопок идут сверху вниз в неубывающем порядке. Как сделать из этих стопок одну? На каждом шаге мы берём меньшую из двух верхних карт и кладём её (рубашкой вверх) в результирующую стопку. Когда одна из оставшихся стопок становится пустой, мы добавляем все оставшиеся карты второй стопки к результирующей стопке.
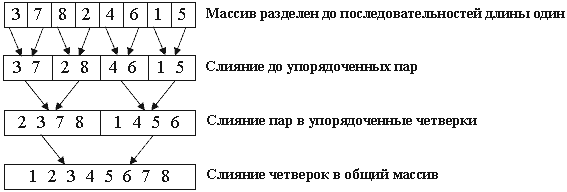
Пример работы алгоритма на массиве 3 7 8 2 4 6 1 5..

Рекурсивный алгоритм обходит получившееся дерево слияния в прямом порядке. Каждый уровень представляет собой проход сортировки слияния - операцию, полностью переписывающую массив.
Обратим внимание, что деление происходит до массива из единственного элемента. Такой массив можно считать упорядоченным, а значит, задача сводится к написанию функции слияния merge.
Один из способов состоит в слиянии двух упорядоченных последовательностей при помощи вспомогательного буфера, равного по размеру общему количеству имеющихся в них элементов. Элементы последовательностей будут перемещаться в этот буфер по одному за шаг.
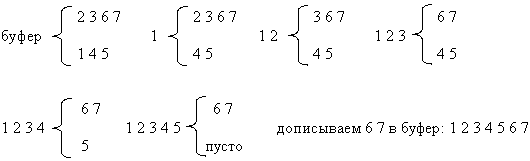
Ну что же, хватит слов, давайте реализовывать!)
def mergeSort(a, lb=0, ub=-1):
def merge(a, lb, split, ub):
#Слияние упорядоченных частей массива в буфер temp
#с дальнейшим переносом содержимого temp в a[lb]...a[ub]
#текущая позиция чтения из первой последовательности a[lb]...a[split]
pos1=lb
#текущая позиция чтения из второй последовательности a[split+1]...a[ub]
pos2=split+1
#текущая позиция записи в temp
pos3=0
temp = [i for i in xrange(ub-lb+1)]
#идет слияние, пока есть хоть один элемент в каждой последовательности
while pos1 <= split and pos2 <= ub:
if a[pos1] < a[pos2]:
temp[pos3] = a[pos1]
pos1+=1
pos3+=1
else:
temp[pos3] = a[pos2]
pos2+=1
pos3+=1
#одна последовательность закончилась -
#копировать остаток другой в конец буфера
while pos2 <= ub: #пока вторая последовательность непуста
temp[pos3] = a[pos2]
pos3+=1
pos2+=1
while pos1 <= split: #пока первая последовательность непуста
temp[pos3] = a[pos1]
pos3+=1
pos1+=1
#скопировать буфер temp в a[lb]...a[ub]
a[lb:ub+1] = temp
del(temp)
if lb < ub:#если есть более 1 элемента
split = (lb + ub)/2# индекс, по которому делим массив
mergeSort(a, lb, split)#сортировать левую половину
mergeSort(a, split+1, ub)##сортировать правую половину
merge(a, lb, split, ub)#слить результаты в общий массив
Оценим быстродействие алгоритма: время работы определяется рекурсивной формулой T(n) = 2T(n/2) + Theta(n).
Ее решение: T(n) = n log n - результат весьма неплох, учитывая отсутствие "худшего случая". Однако, несмотря на хорошее общее быстродействие, у сортировки слиянием есть и серьезный минус: она требует Theta(n) памяти.
Это был классический вариант с сайта алголист. Теперь я приведу пример 2-го алгоритма без дополнительного буфера и рекурсии. Но к сожалению всё вкусно не бывает, поэтому за всё нужно платить. Об этом смотри в результатах. А пока идея:
Она достаточно проста, но не так тривиальна, как в предыдущем алгоритме. Избавившись от рекурсии, мы обязаны следить за следованием промежуточных разбиений самостоятельно. Алгоритм начинает с того, что сравнивает каждые 2 соседних, объединяя их в 1 упорядоченный подмассив. Потом снова 2 соседних(но в каждом из них уже по 2 эл-та), потом так же, но по 4, 8, 16 и т.д. И чтобы не использовать буфер, мы итерационно переставляем элемента прям в памяти, , чтобы упорядочить их(это требует огромного числа перестановок((()
def MergerSort(a):
def MergerGroup(a, left, m, right):
if left >= right: return None
if m < left or right < m: return None
t = left
for j in xrange(m+1, right+1):#подгруппа 2
for i in xrange(t, j):#цикл подгруппы 1
if a[j] < a[i]:
r = a[j]
#итерационно переставляем элементы, чтобы упорядочить
for k in xrange(j, i, -1):
a[k] = a[k - 1]
a[i] = r
t = i#проджолжение вставки в группе 1
break#к следующему узлу из подгруппы 2
if len(a) < 2: return None
k=1
while k<len(a):
g=0
while g<len(a):#группы
z = g + k + k - 1#последний эл-т группы
r = z if z < len(a) else len(a) - 1#последняя группа
MergerGroup(a, g, g + k - 1, r)#слияние
g+=2*k
k*=2
Еще 1 пример не рекурсивного алгоритма приведён на сайте википедии. Но там всё же вводится дополнительный буфер, равный размеру! массива.
Производительность
Тестирование проводилось на списке из 5000 не повторяющихся элементов(как и в быстрой сортировке Хоара, чтобы можно было сравнить).
- первый алгоритм рекурсивный и с дополнительной памятью mergeSort 15002 function calls (5004 primitive calls) in 0.132 seconds
- второй алгоритм не рекурсивный и без доп. буфера MergerSort 15057 function calls in 0.736 seconds
Хорошо запрограммированная внутренняя сортировка слиянием работает немного быстрее пирамидальной, но медленнее быстрой, при этом требуя много памяти под буфер. Поэтому mergeSort используют для упорядочения массивов, лишь если требуется устойчивость метода(которой нет ни у быстрой, ни у пирамидальной сортировок).
Сортировка слиянием является одним из наиболее эффективных методов для односвязных списков и файлов, когда есть лишь последовательный доступ к элементам.


У меня не работает первый код:
ОтветитьУдалитьdata=range(10)
random.shuffle(data)
data1=data[:]
data2=data[:]
data1.sort()
mergeSort(data2)
print data
print data1
print data2
[1, 2, 5, 4, 3, 9, 8, 7, 0, 6]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 5, 4, 3, 9, 8, 7, 0, 6]
Действительно, обязательны все 3 аргумента.
УдалитьЗапустите так - mergeSort(data2, 0, len(data2)-1)